题目内容
16.已知集合M={x|x2+x-2=0,x∈R},N={x|x<0,x∈R},则M∩N=( )| A. | ϕ | B. | {1} | C. | {-2} | D. | {-2,1} |
分析 解方程得集合M,根据交集的定义写出M∩N.
解答 解:集合M={x|x2+x-2=0,x∈R}={x|x=-2或x=1},
N={x|x<0,x∈R},
则M∩N={-2}.
故选:C.
点评 本题考查了集合的化简与运算问题,是基础题.

练习册系列答案
相关题目
3.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为( )
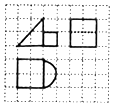

| A. | $\frac{8}{3}$+2π | B. | 4+4$\sqrt{2}$+3π | C. | 8+4$\sqrt{2}$+3π | D. | 10+4$\sqrt{2}$+2π |
5.如图,若n=4时,则输出的结果为( )


| A. | $\frac{3}{7}$ | B. | $\frac{6}{7}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{11}$ |
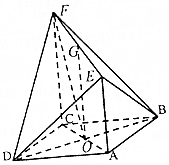 如图,四边形ABCD为菱形,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF⊥平面ABCD,AB=AE=2,G为EF中点.
如图,四边形ABCD为菱形,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF⊥平面ABCD,AB=AE=2,G为EF中点.