题目内容
18.已知角α=390°(1)角α的终边在第几象限;
(2)写出与角α终边相同的角的集合;
(3)在-360°~720°范围内,写出与α终边相同的角.
分析 利用终边相同的角的集合进行表示和求解即可.
解答 解:(1)∵390°=360°+30°,30°是第一象限角,
∴角α的终边在第一象限;
(2)所有和角α终边相同的角的集合为{β|β=k•360°+30°,k∈Z};
(3)∵β=k•360°+30°,
∴当k=-1时,β=-330°,
当k=0时,β=30°,
当k=1时,β=390°,
∴在-360°~720°范围内,与α终边相同的角是-330°,30°,390°.
点评 本题主要考查角的终边相同的求解,根据角终边相同的角的关系是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知随机变量ξ的分布列为:
若$P({ξ^2}<x)=\frac{11}{12}$,则实数x的取值范围是( )
| ξ | -2 | -1 | 0 | 1 | 2 | 3 |
| P | $\frac{1}{12}$ | $\frac{3}{12}$ | $\frac{4}{12}$ | $\frac{1}{12}$ | $\frac{2}{12}$ | $\frac{1}{12}$ |
| A. | 4<x≤9 | B. | 4≤x<9 | C. | x<4或x≥9 | D. | x≤4或x>9 |
6.已知f(x+y)=f(x)+f(y)且f(1)=2,则f(1)+f(2)+…+f(n)不能等于( )
| A. | f(1)+2f(1)+…+nf(1) | B. | f($\frac{n(n+1)}{2}$) | C. | n(n+1) | D. | n(n+1)f(1) |
3.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为( )
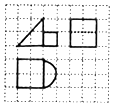

| A. | $\frac{8}{3}$+2π | B. | 4+4$\sqrt{2}$+3π | C. | 8+4$\sqrt{2}$+3π | D. | 10+4$\sqrt{2}$+2π |
7.若a=30.3,b=logπ3,c=log0.3e,则( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | b>c>a |