题目内容
12.已知函数f(x)=lnx+x2-ax(a∈R).(Ⅰ)当a=3时,求函数f(x)的单调区间;
(Ⅱ)若函数f(x)有两个极值点x1,x2,且x1∈(0,1],证明f(x1)-f(x2)≥-$\frac{3}{4}$+ln2.
分析 (Ⅰ)当a=3时,求导数,利用导数的正负,即可求函数f(x)的单调区间;
(Ⅱ)函数f(x)有两个极值点x1,x2,求出函数的导数,问题转化为2x2-ax+1=0有两个不相等的实数根,结合韦达定理,可得f(x1)-f(x2),构造新函数,确定其单调性,即可得出结论.
解答 (Ⅰ)解:f(x)的定义域为(0,+∞),f′(x)=$\frac{{2x}^{2}-3x+1}{x}$,
令f′(x)>0,可得0<x<$\frac{1}{2}$或x>1,f′(x)<0,可得$\frac{1}{2}$<x<1,
∴f(x)的递增区间为(0,$\frac{1}{2}$)和(1,+∞),递减区间为($\frac{1}{2}$,1);
(Ⅱ)证明:∵函数f(x)有两个极值点x1,x2,
∴f′(x)=$\frac{{2x}^{2}-ax+1}{x}$=0,即2x2-ax+1=0有两个不相等的实数根,
∴x1+x2=$\frac{a}{2}$,x1x2=$\frac{1}{2}$,
∴2(x1+x2)=a,x2=$\frac{1}{{2x}_{1}}$,
∴f(x1)-f(x2)=lnx1+x12-ax1-(lnx2+x22-ax2)=2lnx1-x12+$\frac{1}{{{4x}_{1}}^{2}}$+ln2(0<x≤1).
设F(x)=2lnx-x2+$\frac{1}{{4x}^{2}}$+ln2(0<x≤1),则F′(x)=-$\frac{{({2x}^{2}-1)}^{2}}{{2x}^{3}}$<0,
∴F(x)在(0,1)上单调递减,
∴F(x)≥F(1)=-$\frac{3}{4}$+ln2,即f(x1)-f(x2)≥-$\frac{3}{4}$+ln2.
点评 本题考查导数的综合运用,考查函数的单调性,考查不等式的证明,考查分类讨论的数学思想.

 新思维寒假作业系列答案
新思维寒假作业系列答案
| A. | $\frac{8}{3}$+2π | B. | 4+4$\sqrt{2}$+3π | C. | 8+4$\sqrt{2}$+3π | D. | 10+4$\sqrt{2}$+2π |
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | b>c>a |
| A. | y2=8$\sqrt{5}$x | B. | y2=4$\sqrt{5}$x | C. | y2=2$\sqrt{5}$x | D. | y2=$\sqrt{5}$x |

| A. | $\frac{3}{7}$ | B. | $\frac{6}{7}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{11}$ |
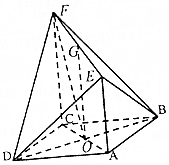 如图,四边形ABCD为菱形,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF⊥平面ABCD,AB=AE=2,G为EF中点.
如图,四边形ABCD为菱形,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF⊥平面ABCD,AB=AE=2,G为EF中点.