题目内容
11．在空间直角坐标系中，点A（1，0，1）和点B（2，1，-1）间的距离$\sqrt{6}$．分析 直接利用空间两点间的距离公式求解即可．
解答 解：空间直角坐标系中的点A（1，0，1）和点B（2，1，-1）间的距离：$\sqrt{（2-1）^{2}+（1-0）^{2}+（-1-1）^{2}}$=$\sqrt{6}$．
故答案为$\sqrt{6}$．
点评 本题考查空间两点间的距离公式的应用，基本知识的考查．
练习册系列答案
相关题目
1．已知集合A={-2，0，2}，B={x|x2+x-2=0}，则A∩B=（ ）
| A． | ∅ | B． | {2} | C． | {0} | D． | {-2} |
6．已知f（x+y）=f（x）+f（y）且f（1）=2，则f（1）+f（2）+…+f（n）不能等于（ ）
| A． | f（1）+2f（1）+…+nf（1） | B． | f（$\frac{n（n+1）}{2}$） | C． | n（n+1） | D． | n（n+1）f（1） |
16．
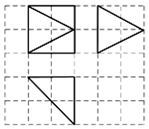如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，几何体的表面积为（ ）
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，几何体的表面积为（ ）| A． | 4+2（$\sqrt{2}$+$\sqrt{3}$） | B． | 6+2（$\sqrt{2}$+$\sqrt{5}$） | C． | 10 | D． | 12 |
3．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的表面积为（ ）
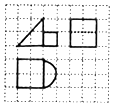
| A． | $\frac{8}{3}$+2π | B． | 4+4$\sqrt{2}$+3π | C． | 8+4$\sqrt{2}$+3π | D． | 10+4$\sqrt{2}$+2π |