题目内容
已知函数f(x)=
,若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是( )
|
| A、(2,2014) |
| B、(2,2015) |
| C、(3,2014) |
| D、(3,2015) |
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:先判断函数的性质以及图象的特点,利用数形结合的思想去解决.
解答:
解:当0≤x<1时,函数f(x)=-4x2+4x=-4(x-
)2+1,函数的对称轴为x=
.
当x=1时,由log2014x=1,解得x=2014.
若a,b,c互不相等,不妨设a<b<c,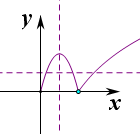
因为f(a)=f(b)=f(c),
所以由图象可知0<a<
,
<b<1,1<c<2014,
且
=
,即a+b=1,
所以a+b+c=1+c,
因为1<c<2014,
所以2<1+c<2015,
即2<a+b+c<2015,
所以a+b+c的取值范围是(2,2015).
故选B.
| 1 |
| 2 |
| 1 |
| 2 |
当x=1时,由log2014x=1,解得x=2014.
若a,b,c互不相等,不妨设a<b<c,

因为f(a)=f(b)=f(c),
所以由图象可知0<a<
| 1 |
| 2 |
| 1 |
| 2 |
且
| a+b |
| 2 |
| 1 |
| 2 |
所以a+b+c=1+c,
因为1<c<2014,
所以2<1+c<2015,
即2<a+b+c<2015,
所以a+b+c的取值范围是(2,2015).
故选B.
点评:本题主要考查函数与方程的应用,考查二次函数的对称性,利用数形结合是解决本题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
定义在R上的奇函数f(x)在(0,+∞)上单调递减,f(
)=0,△ABC的内角A满足f(cosA)≤0,则A的取值范围是( )
| 1 |
| 2 |
A、[
| ||||||||
B、[
| ||||||||
C、(0,
| ||||||||
D、[0,
|
已知函数f(x)=
,若f(a)=
,则f(-a)=( )
| x2+x+1 |
| x2+1 |
| 1 |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
若复数(m2-1)+(m+1)i为实数(i为虚数单位),则实数m的值为( )
| A、-1 | B、0 | C、1 | D、-1或1 |
已知集合A={x|x2-
x+1=0},若A∩R=∅,则实数m的取值范围为( )
| m |
| A、m<4 | B、m>4 |
| C、0<m<4 | D、0≤m<4 |
已知x∈[-
,
],则函数y=sin4x-cos4x的最小值是( )
| π |
| 12 |
| π |
| 3 |
| A、-1 | ||||
B、-
| ||||
C、
| ||||
| D、1 |
已知定义域为R的函数f(x)在(0,+∞)上为增函数,且函数f(x)为偶函数,则下列结论成立的是 ( )
| A、f(0)>f(1) |
| B、f(0)>f(2) |
| C、f(-1)>f(2) |
| D、f(-3)>f(1) |