题目内容
已知抛物线C:y2=x.命题p:直线l1:y=kx+1与抛物线C有公共点.命题q:直线l2:y=k(x-
)被抛物线C所截得的线段长大于2.若p∧q为假,p∨q为真,求k的取值范围.
| 1 |
| 4 |
考点:复合命题的真假
专题:简易逻辑
分析:分别判断命题p,q的真假,根据复合命题之间的关系即可得到结论.
解答:
解:若p为真,联立C和l1的方程化简得k2x+(2k-1)x+1=0.k=0时,方程显然有解;
k≠0时,由△≥0得k≤
且k≠0.综上k≤
,
若q为真,联立C和l2的方程化简得k2x2-(
+1)x+
=0,k=0时显然不成立;
∴x1+x2=
+
,
由于l2是抛物线的焦点弦,故|AB|=x1+x2+p=1+
>2,解得-1<k<1且k≠0.
∵若p∧q为假,p∨q为真,∴p,q一真一假.
若p真q假,则k≤-1或k=0; 若q真p假,则
<k<1.
综上k≤-1或k=0或
<k<1.
k≠0时,由△≥0得k≤
| 1 |
| 4 |
| 1 |
| 4 |
若q为真,联立C和l2的方程化简得k2x2-(
| k2 |
| 2 |
| k2 |
| 16 |
∴x1+x2=
| 1 |
| 2 |
| 1 |
| k2 |
由于l2是抛物线的焦点弦,故|AB|=x1+x2+p=1+
| 1 |
| k2 |
∵若p∧q为假,p∨q为真,∴p,q一真一假.
若p真q假,则k≤-1或k=0; 若q真p假,则
| 1 |
| 4 |
综上k≤-1或k=0或
| 1 |
| 4 |
点评:本题主要考查复合命题的真假应用,分别判断命题p,q的真假是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若复数(m2-1)+(m+1)i为实数(i为虚数单位),则实数m的值为( )
| A、-1 | B、0 | C、1 | D、-1或1 |
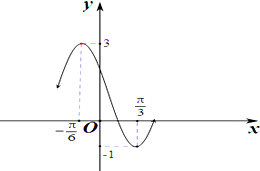 已知函数g(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<
已知函数g(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<