题目内容
1．在正方体ABCD-A1B1C1D1中，M和N分别为A1B1和B1C1的中点，那么直线AM与CN所成角的余弦值是 （ ）| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $\frac{{\sqrt{10}}}{10}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
分析 取AB中点E，BC中点F，连接B1E，B1F，则∠EB1F为直线AM与CN所成角，设正方体棱长为2a，然后利用余弦定理求解．
解答 解：如图，
取AB中点E，BC中点F，连接B1E，B1F，
则四边形AEB1M，B1FCN为平行四边形，
∴AM∥B1E，CN∥B1F，
∴∠EB1F为直线AM与CN所成角（或补角），
设正方体的棱长为2a，则BE=BF=a，EF=$\sqrt{2}a$，${B}_{1}E={B}_{1}F=\sqrt{5}a$，
∴cos∠EB1F=$\frac{（\sqrt{5}a）^{2}+（\sqrt{5}a）^{2}-（\sqrt{2}a）^{2}}{2×\sqrt{5}a×\sqrt{5}a}$=$\frac{4}{5}$．
∴直线AM与CN所成角的余弦值是$\frac{4}{5}$．
故选：D．
点评 本题考查异面直线所成的角，关键是找出角，是中档题．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
把自然数按如图所示排列起来，从上往下依次为第一行、第二行、第三行…，中间用虚线围起来的一列数，从上往下依次为1、5、13、25、…，按这样的顺序，排在第30个的数是1741．
12．如果$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}{ax+by=1}\\{bx+ay=2}\end{array}\right.$的解，那么a，b的值是（ ）
| A． | $\left\{\begin{array}{l}{a=-1}\\{b=0}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{a=1}\\{b=0}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{a=0}\\{b=1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{a=0}\\{b=-1}\end{array}\right.$ |
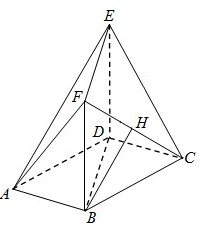如图，在多面体ABCDEF中，底面ABCD是边长为2的菱形，∠BAD=60°，四边形BDEF是矩形，平面BDEF⊥平面ABCD，BF=3，H是CF的中点．
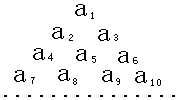已知数列{an}是首项为1，公差为2的等差数列，将数列{an}中的各项排成如图所示的一个三角形数表，记A（i，j）表示第i行从左至右的第j个数，例如A（4，3）=a9，则A（10，2）=93．
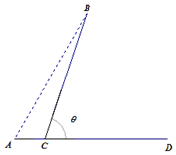某城市A计划每天从蔬菜基地B处给本市供应蔬菜，为此，准备从主干道AD的C处（不在端点A、D处）做一条道路CB，主干道AD的长为60千米，设计路线如图所示，测得蔬菜基地B在城市A的东偏北60°处，AB长为60千米，设∠BCD=θ，运输汽车在主干道AD上的平均车速为60千米/小时，在道路CB上的平均车速为20千米/小时．
13．已知函数f（x）=e2-x+x，x∈[1，3]，则下列说法正确的是（ ）
| A． | 函数f（x）的最大值为$3+\frac{1}{e}$ | B． | 函数f（x）的最小值为$3+\frac{1}{e}$ | ||
| C． | 函数f（x）的最大值为3 | D． | 函数f（x）的最小值为3 |
10．将正奇数按如下规律填在5列的数表中：则2015排在该表的第252行，第1列．（行是从上往下数，列是从左往右数）．
| 1 | 3 | 5 | 7 | |
| 15 | 13 | 11 | 9 | |
| 17 | 19 | 21 | 23 | |
| 31 | 29 | 27 | 25 | |
| … | … | … | … | … |