题目内容
11．
把自然数按如图所示排列起来，从上往下依次为第一行、第二行、第三行…，中间用虚线围起来的一列数，从上往下依次为1、5、13、25、…，按这样的顺序，排在第30个的数是1741．
分析 中间用虚线围的一列，从上至下，相邻两个数都相差4，由此可求出第30个数．
解答 解：中间用虚线围的一列，从上至下：
第一个数为1，
第二个数为5=1+4×1，
第三个数为13=1+4×1+4×2，
第四个数为25=1+4×1+4×2+4×3，
…，
则第30个数为1+4×1+4×2+4×3+…+4×29
=1+4（1+2+3+…+29）=1+4×$\frac{29×30}{2}$=1741．
故答案为1741
点评 本题属于规律探究题，关注相邻两个数之间的关系是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
19．设a＞0且a≠1，函数f（x）=loga|x2-（a+$\frac{1}{a}}）x+1}$）x+1|在[1，2]上是增函数，则a的取值范围（ ）
| A． | a≥2+$\sqrt{3}$ | B． | 0＜a＜2-$\sqrt{3}$ | C． | a≥2+$\sqrt{3}$或0＜a＜1 | D． | a≥2+$\sqrt{3}$或0＜a＜2-$\sqrt{3}$ |
6．已知向量$\overrightarrow{a}$=（1，$\sqrt{3}$），$\overrightarrow{b}$=（$\sqrt{3}$，1），则$\overrightarrow{a}$与$\overrightarrow{b}$夹角的大小为（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
20．
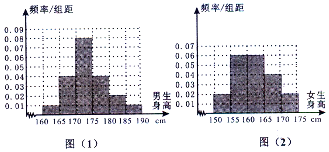某学校为调查高三年学生的身高情况，按随机抽样的方法抽取80名学生，得到男生身高情况的频率分布直方图（图（1）和女生身高情况的频率分布直方图（图（2））．已知图（1）中身高在170～175cm的男生人数有16人．
（I）试问在抽取的学生中，男、女生各有多少人？
（II）根据频率分布直方图，完成下列的2×2列联表，并判断能有多大的把握认为“身高与性别有关”？
参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
某学校为调查高三年学生的身高情况，按随机抽样的方法抽取80名学生，得到男生身高情况的频率分布直方图（图（1）和女生身高情况的频率分布直方图（图（2））．已知图（1）中身高在170～175cm的男生人数有16人．（I）试问在抽取的学生中，男、女生各有多少人？
（II）根据频率分布直方图，完成下列的2×2列联表，并判断能有多大的把握认为“身高与性别有关”？
| ≥170cm | ＜170cm | 总计 | |
| 男生身高 | 30 | 10 | 40 |
| 女生身高 | 4 | 36 | 40 |
| 总计 | 34 | 46 | 80 |
| p（K2＞k） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.445 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
1．在正方体ABCD-A1B1C1D1中，M和N分别为A1B1和B1C1的中点，那么直线AM与CN所成角的余弦值是 （ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $\frac{{\sqrt{10}}}{10}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |