题目内容
18. 如图,“赵爽弦图”是由四个全等的直角三角形(阴影部分)围成一个大正方形,中间空出一个小正方形组成的图形,若在大正方形内随机取一点,该点落在小正方形的概率为$\frac{1}{5}$,则图中直角三角形中较大锐角的正弦值为( )
如图,“赵爽弦图”是由四个全等的直角三角形(阴影部分)围成一个大正方形,中间空出一个小正方形组成的图形,若在大正方形内随机取一点,该点落在小正方形的概率为$\frac{1}{5}$,则图中直角三角形中较大锐角的正弦值为( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 求出四个全等的直角三角形的三边的关系,从而求出sinθ的值即可.
解答 解:在大正方形内随机取一点,这一点落在小正方形的概率为$\frac{1}{5}$,
不妨设大正方形面积为5,小正方形面积为1,
∴大正方形边长为$\sqrt{5}$,小正方形的边长为1.
∴四个全等的直角三角形的斜边的长是$\sqrt{5}$,
较短的直角边的长是1,较长的直角边的长是2,
故sinθ=$\frac{2}{\sqrt{5}}=\frac{2\sqrt{5}}{5}$,
故选:B.
点评 本题考查了几何概型问题,考查三角函数问题,是一道基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知抛物线C:y2=4x,过焦点F且斜率为$\sqrt{3}$的直线与C相交于P,Q两点,且P,Q两点在准线上的投影分别为M,N两点,则S△MFN=( )
| A. | $\frac{8}{3}$ | B. | $\frac{{8\sqrt{3}}}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{{16\sqrt{3}}}{3}$ |
3.执行如图的程序框图,则输出的S=( )

| A. | 2 | B. | -3 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{3}$ |
10.已知等腰梯形ABCD中AB∥CD,AB=2CD=4,∠BAD=60°,双曲线以A,B为焦点,且经过C,D两点,则该双曲线的离心率等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}+1$ |
7.如图是秦九韶算法的一个程序框图,则输出的S为( )
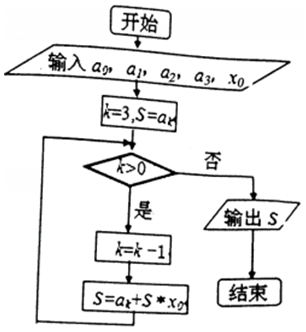

| A. | a1+x0(a3+x0(a0+a2x0))的值 | B. | a3+x0(a2+x0(a1+a0x0))的值 | ||
| C. | a0+x0(a1+x0(a2+a3x0))的值 | D. | a2+x0(a0+x0(a3+a1x0))的值 |
8.在数列{an}中,a1=1,a2=2,且${a_{n+2}}-{a_n}=1+{(-1)^n}$(n∈N+),则S100=( )
| A. | 0 | B. | 1300 | C. | 2600 | D. | 2602 |