题目内容
8.在数列{an}中,a1=1,a2=2,且${a_{n+2}}-{a_n}=1+{(-1)^n}$(n∈N+),则S100=( )| A. | 0 | B. | 1300 | C. | 2600 | D. | 2602 |
分析 奇数项:a2k+1=1+(-1)2k-1+a2k-1=a2k-1,偶数项:a2k+2=1+(-1)2k+a2k=2+a2k,所以奇数项相等,偶数项为等差数列,公差为2,由此能求出S奇数项:a2k+1=1+(-1)2k-1+a2k-1=a2k-1,故能求出S100.
解答 解:奇数项:a2k+1=1+(-1)2k-1+a2k-1=a2k-1,
偶数项:a2k+2=1+(-1)2k+a2k=2+a2k
所以奇数项相等,偶数项为等差数列,公差为2
a100=a2+49×2=100,
S100=50×a1+50×(a1+a100)×$\frac{1}{2}$
=50+50(2+100)×$\frac{1}{2}$=2600.
故选:C.
点评 本题考查数列的递推式,解题时要注意分类思想的合理运用.

练习册系列答案
相关题目
18. 如图,“赵爽弦图”是由四个全等的直角三角形(阴影部分)围成一个大正方形,中间空出一个小正方形组成的图形,若在大正方形内随机取一点,该点落在小正方形的概率为$\frac{1}{5}$,则图中直角三角形中较大锐角的正弦值为( )
如图,“赵爽弦图”是由四个全等的直角三角形(阴影部分)围成一个大正方形,中间空出一个小正方形组成的图形,若在大正方形内随机取一点,该点落在小正方形的概率为$\frac{1}{5}$,则图中直角三角形中较大锐角的正弦值为( )
 如图,“赵爽弦图”是由四个全等的直角三角形(阴影部分)围成一个大正方形,中间空出一个小正方形组成的图形,若在大正方形内随机取一点,该点落在小正方形的概率为$\frac{1}{5}$,则图中直角三角形中较大锐角的正弦值为( )
如图,“赵爽弦图”是由四个全等的直角三角形(阴影部分)围成一个大正方形,中间空出一个小正方形组成的图形,若在大正方形内随机取一点,该点落在小正方形的概率为$\frac{1}{5}$,则图中直角三角形中较大锐角的正弦值为( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{\sqrt{3}}{3}$ |
13.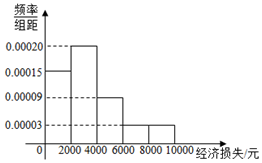 2016年10月21日,台风“海马”导致江苏、福建、广东3省11市51个县(市、区)189.9万人受灾,某调查小组调查了受灾某小区的100户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图.
2016年10月21日,台风“海马”导致江苏、福建、广东3省11市51个县(市、区)189.9万人受灾,某调查小组调查了受灾某小区的100户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图.
(Ⅰ)台风后居委会号召小区居民为台风重灾区捐款,小张调查的100户居民捐款情况如表所示,在表格空白处填写正确数字,并说明能否在犯错误的概率不超过0.05的前提下认为捐款数额超过或不超过500元和自身经济损失是否超过4000元有关?
(Ⅱ)将上述调查所得到的频率视为概率,现在从该地区大量受灾居民中,采用随机抽样的方法每次抽取1户居民,抽取3次,记被抽取的3户居民中自身经济损失超过4000元的人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列,期望E(ξ)和方差D(ξ).
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
 2016年10月21日,台风“海马”导致江苏、福建、广东3省11市51个县(市、区)189.9万人受灾,某调查小组调查了受灾某小区的100户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图.
2016年10月21日,台风“海马”导致江苏、福建、广东3省11市51个县(市、区)189.9万人受灾,某调查小组调查了受灾某小区的100户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图.(Ⅰ)台风后居委会号召小区居民为台风重灾区捐款,小张调查的100户居民捐款情况如表所示,在表格空白处填写正确数字,并说明能否在犯错误的概率不超过0.05的前提下认为捐款数额超过或不超过500元和自身经济损失是否超过4000元有关?
(Ⅱ)将上述调查所得到的频率视为概率,现在从该地区大量受灾居民中,采用随机抽样的方法每次抽取1户居民,抽取3次,记被抽取的3户居民中自身经济损失超过4000元的人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列,期望E(ξ)和方差D(ξ).
| 经济损失不超过4000元 | 经济损失超过4000元 | 总计 | |
| 捐款超过500元 | 60 | ||
| 捐款不超过500元 | 10 | ||
| 总计 |
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
20.为调查我市居民对“文明出行”相关规定的了解情况,某媒体随机选取了30名行人进行问卷调查,将他们的年龄整理后分组,制成下表:
己知从中任选一人,年龄在(12,22]的频率为0.3
(I)求m,n的值;
(II)通过问卷得知,参与调查的52岁以上的两个组中,了解相关规定的人各占$\frac{1}{2}$.现从这两个组中任选2人,求选取的2人都了解相关规定的概率.
| 年龄(岁) | (12,22] | (22,32] | (32,42] | (42,52] | (52,62] | (62,72] |
| 频数 | m | 3 | 7 | 5 | 4 | n |
(I)求m,n的值;
(II)通过问卷得知,参与调查的52岁以上的两个组中,了解相关规定的人各占$\frac{1}{2}$.现从这两个组中任选2人,求选取的2人都了解相关规定的概率.
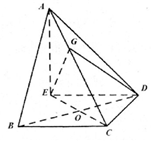 如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.
如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.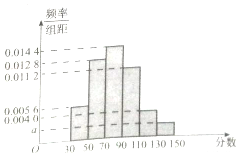 某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)
某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)