题目内容
在平面直角坐标系中,O为坐标原点,|
|=|
|=|
|=1,
+
+
=
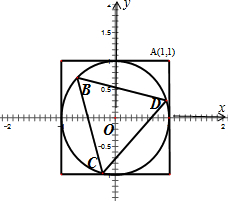
,A(1,1),则
•
的取值范围( )
| OB |
| OC |
| OD |
| OB |
| OC |
| OD |
| 0 |
| AD |
| OB |
A、[-1-
| ||||||||
B、[-
| ||||||||
C、[
| ||||||||
D、[1-
|
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:由三角形的外心和重心的概念,可得O既是外心也为重心,则有△BCD为圆O:x2+y2=1的内接等边三角形,
又
•
=(
-
)•
,由向量的数量积的定义和余弦函数的值域,即可得到所求范围.
又
| AD |
| OB |
| OD |
| OA |
| OB |
解答:
 解:由|
解:由|
|=|
|=|
|=1,可知O为外心,
由
+
+
=
,可知O又为重心.
则有△BCD为圆O:x2+y2=1的内接等边三角形,
即有
•
=(
-
)•
=
•
-
•
=|
|•|
|cos120°-|
|•|
|cos<
,
>
=-
-
cos<
,
>,由于0≤<
,
>≤π,
则-1≤cos<
,
>≤1,
即有
•
∈[-
-
,-
+
].
故选:B.
 解:由|
解:由|| OB |
| OC |
| OD |
由
| OB |
| OC |
| OD |
| 0 |
则有△BCD为圆O:x2+y2=1的内接等边三角形,
即有
| AD |
| OB |
| OD |
| OA |
| OB |
| OD |
| OB |
| OA |
| OB |
=|
| OD |
| OB |
| OA |
| OB |
| OA |
| OB |
=-
| 1 |
| 2 |
| 2 |
| OA |
| OB |
| OA |
| OB |
则-1≤cos<
| OA |
| OB |
即有
| AD |
| OB |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
故选:B.
点评:本题考查向量的数量积的定义,主要考查余弦函数的值域,运用三角形的外心和重心的定义和向量的三角形法则是解题的关键.

练习册系列答案
相关题目
已知命题p:?x0∈R,cosx0≤
,则?p是( )
| 1 |
| 2 |
A、?x0∈R,cosx0≥
| ||
B、?x0∈R,cosx0>
| ||
C、?x∈R,cosx≥
| ||
D、?x∈R,cosx>
|
定义域为R的函数f(x)满足f(x+2)=2f(x)-2,当x∈(0,2]时,f(x)=
,若x∈(0,4]时,t2-
≤f(x)恒成立,则实数t的取值范围是( )
|
| 7t |
| 2 |
| A、[1,2] | ||
B、[2,
| ||
C、[1,
| ||
| D、[2,+∞) |
已知实数2、t、8构成一个等比数列,则圆锥曲线
+y2=1的离心率为( )
| x2 |
| t |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|