题目内容
以下四个命题:
①在等差数列{an}中,Sn是其前n项和,则Sn,S2n-Sn,S3n-S2n仍成等差数列;
②在等比数列{an}中,Sn是其前n项和,则Sn,S2n-Sn,S3n-S2n仍成等比数列;
③函数y=x与y=sinx在(-
,
)上的图象有3个不同的交点;
④命题甲:x≠2或y≠3;命题乙:x+y≠5,则甲是乙的必要不充分条件.
其中真命题的序号有 .
①在等差数列{an}中,Sn是其前n项和,则Sn,S2n-Sn,S3n-S2n仍成等差数列;
②在等比数列{an}中,Sn是其前n项和,则Sn,S2n-Sn,S3n-S2n仍成等比数列;
③函数y=x与y=sinx在(-
| π |
| 2 |
| π |
| 2 |
④命题甲:x≠2或y≠3;命题乙:x+y≠5,则甲是乙的必要不充分条件.
其中真命题的序号有
考点:命题的真假判断与应用
专题:综合题,推理和证明
分析:①利用等差数列的求和公式,可得①正确;
②利用等比数列的特例判断选项是否正确;
③利用三角函数线与角的弧度数的大小,判断③是否正确;
④我们可先判断x≠2或y≠3时,x+y≠5是否成立,再判断x+y≠5时,x≠2或y≠3是否成立,再根据充要条件的定义即可得到结论.
②利用等比数列的特例判断选项是否正确;
③利用三角函数线与角的弧度数的大小,判断③是否正确;
④我们可先判断x≠2或y≠3时,x+y≠5是否成立,再判断x+y≠5时,x≠2或y≠3是否成立,再根据充要条件的定义即可得到结论.
解答:
解:对于①,利用等差数列的求和公式,可得①正确;
对于②,设an=(-1)n,则S2=0,S4-S2=0,S6-S4=0,∴此数列不是等比数列,故不正确
对于③,根据正弦线|sinx|≤|x|当且仅当x=0取“=”,∴只有一个交点,故③不正确;
对④,若x≠2或y≠3时,如x=1,y=4,则x+y=5,即x+y≠5不成立,故命题甲:x≠2或y≠3⇒命题乙:x+y≠5为假命题;若x=2,y=3成立,则x+y=5一定成立,即x=2,y=3⇒x+y=5为真命题,根据互为逆否命题真假性相同,故命题乙:x+y≠5⇒命题甲:x≠2或y≠3也为真命题,故甲是乙的必要非充分条件,故正确.
故答案为:①④.
对于②,设an=(-1)n,则S2=0,S4-S2=0,S6-S4=0,∴此数列不是等比数列,故不正确
对于③,根据正弦线|sinx|≤|x|当且仅当x=0取“=”,∴只有一个交点,故③不正确;
对④,若x≠2或y≠3时,如x=1,y=4,则x+y=5,即x+y≠5不成立,故命题甲:x≠2或y≠3⇒命题乙:x+y≠5为假命题;若x=2,y=3成立,则x+y=5一定成立,即x=2,y=3⇒x+y=5为真命题,根据互为逆否命题真假性相同,故命题乙:x+y≠5⇒命题甲:x≠2或y≠3也为真命题,故甲是乙的必要非充分条件,故正确.
故答案为:①④.
点评:本题考查命题的真假判断,考查学生分析解决问题的能力,涉及知识点多,综合性强.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
在平面直角坐标系中,O为坐标原点,|
|=|
|=|
|=1,
+
+
=
,A(1,1),则
•
的取值范围( )
| OB |
| OC |
| OD |
| OB |
| OC |
| OD |
| 0 |
| AD |
| OB |
A、[-1-
| ||||||||
B、[-
| ||||||||
C、[
| ||||||||
D、[1-
|
已知D、E分别是△ABC的边AB、AC上的点,且BD=2AD,AE=2EC,点P是线段DE上的任意一点,若
=x
+y
,则xy的最大值为( )
| AP |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
实数x、y满足x2+2xy+y2+4x2y2=4,则x-y的最大值为( )
A、
| ||
B、
| ||
C、
| ||
D、2
|
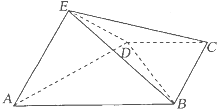 如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,AB=4,BC=CD=EA=ED=2,F是线段EB的中点.
如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,AB=4,BC=CD=EA=ED=2,F是线段EB的中点. 如图,圆内接四边形ABCD的边BC与AD的延长线交于点E,点F在BA的延长线上.
如图,圆内接四边形ABCD的边BC与AD的延长线交于点E,点F在BA的延长线上.