题目内容
定义域为R的函数f(x)满足f(x+2)=2f(x)-2,当x∈(0,2]时,f(x)=
,若x∈(0,4]时,t2-
≤f(x)恒成立,则实数t的取值范围是( )
|
| 7t |
| 2 |
| A、[1,2] | ||
B、[2,
| ||
C、[1,
| ||
| D、[2,+∞) |
考点:分段函数的应用,函数恒成立问题
专题:函数的性质及应用,不等式的解法及应用
分析:由f(x+2)=2f(x)-2,求出x∈(2,3),以及x∈[3,4],的函数的解析式,分别求出(0,4]内的四段的最小值,注意运用二次函数的最值和函数的单调性,再由t2-
≤f(x)恒成立即为由t2-
≤f(x)min,解不等式即可得到所求范围.
| 7t |
| 2 |
| 7t |
| 2 |
解答:
解:当x∈(2,3),则x-2∈(0,1),
则f(x)=2f(x-2)-2=2(x-2)2-2(x-2)-2,即为
f(x)=2x2-10x+10,
当x∈[3,4],则x-2∈[1,2],
则f(x)=2f(x-2)-2=
-2.
当x∈(0,1)时,当x=
时,f(x)取得最小值,且为-
;
当x∈[1,2]时,当x=2时,f(x)取得最小值,且为
;
当x∈(2,3)时,当x=
时,f(x)取得最小值,且为-
;
当x∈[3,4]时,当x=4时,f(x)取得最小值,且为-1.
综上可得,f(x)在(0,4]的最小值为-
.
若x∈(0,4]时,t2-
≤f(x)恒成立,
则有t2-
≤-
.
解得1≤t≤
.
故选:C.
则f(x)=2f(x-2)-2=2(x-2)2-2(x-2)-2,即为
f(x)=2x2-10x+10,
当x∈[3,4],则x-2∈[1,2],
则f(x)=2f(x-2)-2=
| 2 |
| x-2 |
当x∈(0,1)时,当x=
| 1 |
| 2 |
| 1 |
| 4 |
当x∈[1,2]时,当x=2时,f(x)取得最小值,且为
| 1 |
| 2 |
当x∈(2,3)时,当x=
| 5 |
| 2 |
| 5 |
| 2 |
当x∈[3,4]时,当x=4时,f(x)取得最小值,且为-1.
综上可得,f(x)在(0,4]的最小值为-
| 5 |
| 2 |
若x∈(0,4]时,t2-
| 7t |
| 2 |
则有t2-
| 7t |
| 2 |
| 5 |
| 2 |
解得1≤t≤
| 5 |
| 2 |
故选:C.
点评:本题考查分段函数的运用,主要考查分段函数的最小值,运用不等式的恒成立思想转化为求函数的最值是解题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
已知集合A={x|x2-3x+2=0},B={-2,-1,1,2},则A∩B=( )
| A、{-2,-1} |
| B、{-1,2} |
| C、{1,2} |
| D、{-2,-1,1,2} |
已知函数f(x)=
,若g(x)=|f(x)|-ax-a的图象与x轴有3个不同的交点,则实数a的取值范围是( )
|
A、(0,
| ||||
B、(0,
| ||||
C、[
| ||||
D、[
|
在平面直角坐标系中,O为坐标原点,|
|=|
|=|
|=1,
+
+
=
,A(1,1),则
•
的取值范围( )
| OB |
| OC |
| OD |
| OB |
| OC |
| OD |
| 0 |
| AD |
| OB |
A、[-1-
| ||||||||
B、[-
| ||||||||
C、[
| ||||||||
D、[1-
|
已知圆O:x2+y2=1和直线l:y=kx+
,则k=1是圆O与直线l相切的( )
| 2 |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
如图所示的程序框图的输出值y∈(1,2],则输入值x的范围是( )
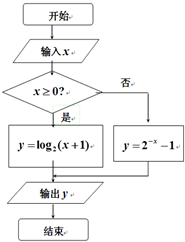

| A、(-∞,3] |
| B、[-1,log23) |
| C、[-log23,-1)∪(1,3] |
| D、[-log23,0)∪(1,3] |
 如图,已知四边形ABCD为正方形,EA⊥平面ABCD,CF∥EA,且EA=
如图,已知四边形ABCD为正方形,EA⊥平面ABCD,CF∥EA,且EA=