Question

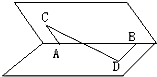如图，在锐二面角α-AB-β内，AC?β，BD?α，AC⊥AB于A，BD⊥AB于B，且AC=BD=2，AB=4，CD=

22

，则二面角α-AB-β的余弦值为

 

．

Answer 1

考点：二面角的平面角及求法

专题：空间角

分析：设二面角α-AB-β的余弦值为cosα，由已知得：

CD

2=(

CA

+

AB

+

BD

)2，从而得到4+16+4-2×2×2cosθ=22，由此能求出二面角α-AB-β的余弦值．

解答： 解：设二面角α-AB-β的余弦值为cosα，
由已知得：

CD

2=(

CA

+

AB

+

BD

)2
=4+16+4-2×2×2cosθ=22，
解得cosθ=

1

4

．
故答案为：

1

4

．

点评：本题考查二面角的余弦值的求法，是中档题，解题时要认真审题，注意向量法的合理运用．