题目内容
四棱锥的三视图如图所示,则此四棱锥的内切球半径为 .


考点:球内接多面体,由三视图还原实物图
专题:计算题,空间位置关系与距离
分析:由题意,四棱锥底面是一个边长是4的正方形,高为2,则斜高为
.根据体积法,得到该几何体的内切球半径.
| 2 |
解答:
解:由题意,四棱锥底面是一个边长是4的正方形,高为2,则斜高为
.
设该几何体的内切球半径为r,则
(16+4×
×4×
)×r=
×16×2
∴r=2
-2.
故答案为:2
-2.
| 2 |
设该几何体的内切球半径为r,则
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 1 |
| 3 |
∴r=2
| 2 |
故答案为:2
| 2 |
点评:本题考查多面体的内切球的运算,这是一个综合题目,解题时注意体积法的应用.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
下列四个关系式中,正确的是( )
| A、∅∈{a} |
| B、a⊆{a} |
| C、{a}∈{a,b} |
| D、a∈{a,b} |
lg2+lg50=( )
| A、1 | B、2 | C、3 | D、4 |
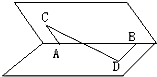 如图,在锐二面角α-AB-β内,AC?β,BD?α,AC⊥AB于A,BD⊥AB于B,且AC=BD=2,AB=4,CD=
如图,在锐二面角α-AB-β内,AC?β,BD?α,AC⊥AB于A,BD⊥AB于B,且AC=BD=2,AB=4,CD=