题目内容
不等式组
表示平面区域的面积是 .
|
考点:二元一次不等式(组)与平面区域
专题:不等式的解法及应用
分析:作出不等式对应的平面区域,利用平面区域的图形求平面区域面积即可.
解答:
解:作出不等式对应的平面区域如图:(阴影部分),
由
,解得
,即B(2,4).
∵4x+3y=20过点C(5,0),x-y=-2过点A(0,2),
∴D(2,0),
∴阴影部分的面积为
+
×3×4=6+6=12.
故答案为:12.
由
|
|

∵4x+3y=20过点C(5,0),x-y=-2过点A(0,2),
∴D(2,0),
∴阴影部分的面积为
| (2+4)×2 |
| 2 |
| 1 |
| 2 |
故答案为:12.
点评:本题主要考查二元一次不等式表示平面区域的计算,根据图象将四边形分解为直角梯形和三角形是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知直线l⊥平面α,直线m?平面β,有下列四个命题
①α∥β⇒l⊥m
②α⊥β⇒l∥m
③l∥m⇒α⊥β
④l⊥m⇒α⊥β
其中正确的两个命题是( )
①α∥β⇒l⊥m
②α⊥β⇒l∥m
③l∥m⇒α⊥β
④l⊥m⇒α⊥β
其中正确的两个命题是( )
| A、①与② | B、③与④ |
| C、②与④ | D、①与③ |
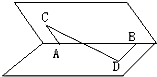 如图,在锐二面角α-AB-β内,AC?β,BD?α,AC⊥AB于A,BD⊥AB于B,且AC=BD=2,AB=4,CD=
如图,在锐二面角α-AB-β内,AC?β,BD?α,AC⊥AB于A,BD⊥AB于B,且AC=BD=2,AB=4,CD=