题目内容
图为一个半球挖去一个圆锥的几何体的三视图,则该几何体的表面积为( )


A、(
| ||||
B、(
| ||||
C、(4+2
| ||||
D、(8+4
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:根据已知中的三视图可得:该几何体是一个半球挖去一个圆锥,其表面积由半球面和圆锥的侧面积组成,由三视图求出球和圆锥底面的半径及圆锥的高,进而求出圆锥的母线长,代入面积公式,可得答案.
解答:
解:如图所示,该几何体的表面积为半球面积与圆锥侧面积之和,
即S=
•4πr2+πrl=8π+4
π=(8+4
)π.
故选:D.
即S=
| 1 |
| 2 |
| 2 |
| 2 |
故选:D.
点评:本题考查学生的空间想象能力,分析出几何体是形状是解答的关键,难度不大,是基础题.

练习册系列答案
相关题目
已知直线l⊥平面α,直线m?平面β,有下列四个命题
①α∥β⇒l⊥m
②α⊥β⇒l∥m
③l∥m⇒α⊥β
④l⊥m⇒α⊥β
其中正确的两个命题是( )
①α∥β⇒l⊥m
②α⊥β⇒l∥m
③l∥m⇒α⊥β
④l⊥m⇒α⊥β
其中正确的两个命题是( )
| A、①与② | B、③与④ |
| C、②与④ | D、①与③ |
lg2+lg50=( )
| A、1 | B、2 | C、3 | D、4 |
函数y=x|x|的图象大致是( )
A、 |
B、 |
C、 |
D、 |
化简
-
的结果是( )
| 1-2sin3cos3 |
| 1+2sin3cos3 |
| A、2cos3 |
| B、2sin3 |
| C、-2sin3 |
| D、-2cos3 |
设集合A={x||x|-1=0},B={x|x2-a≤0},则“a=4”是“A∪B=B”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不必要也不充分条件 |
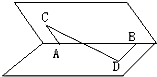 如图,在锐二面角α-AB-β内,AC?β,BD?α,AC⊥AB于A,BD⊥AB于B,且AC=BD=2,AB=4,CD=
如图,在锐二面角α-AB-β内,AC?β,BD?α,AC⊥AB于A,BD⊥AB于B,且AC=BD=2,AB=4,CD=