题目内容
下列各组中表示同一函数的是( )
A、f(x)=x-1,g(x)=
| |||
B、f(x)=x2,g(x)=
| |||
| C、f(x)=1,g(x)=x0 | |||
D、f(x)=x2,g(x)=(
|
考点:判断两个函数是否为同一函数
专题:函数的性质及应用
分析:对于每一个选项中的函数,判定它们的定义域是否相同,对应关系是否也相同,从而判定是否为同一函数.
解答:
解:对于A,f(x)=x-1,x∈R;g(x)=
-1=x-1,x≠0;它们的定义域不同,不是同一函数;
对于B,f(x)=x2,x∈R;g(x)=
=x2,x∈R;它们的定义域相同,对应关系也相同,是同一函数;
对于C,f(x)=1,x∈R;g(x)=x0=1,x≠0;它们的定义域不同,不是同一函数;
对于D,f(x)=x2,x∈R;g(x)=(
)4=x2,x≥0;它们的定义域不同,不是同一函数.
故选:B.
| x2 |
| x |
对于B,f(x)=x2,x∈R;g(x)=
| 3 | x6 |
对于C,f(x)=1,x∈R;g(x)=x0=1,x≠0;它们的定义域不同,不是同一函数;
对于D,f(x)=x2,x∈R;g(x)=(
| x |
故选:B.
点评:本题考查了判定两个函数是否为同一函数的问题,解题时应从定义域和对应关系两个方面进行判定,是基础题.

练习册系列答案
相关题目
下列四个关系式中,正确的是( )
| A、∅∈{a} |
| B、a⊆{a} |
| C、{a}∈{a,b} |
| D、a∈{a,b} |
已知集合P={x,y,z},Q={1,2},映射f:P→Q中满足f(y)=2的映射的个数共有( )
| A、2 | B、4 | C、5 | D、6 |
已知x、y取值如表:
画散点图分析可知:y与x线性相关,且求得回归方程为
=x+1,则m的值(精确到0.1)为( )
| x | 0 | 1 | 4 | 5 | 6 |
| y | 1.3 | m | 3m | 5.6 | 7.4 |
 |
| y |
| A、1.5 | B、1.6 |
| C、1.7 | D、1.8 |
已知直线l⊥平面α,直线m?平面β,有下列四个命题
①α∥β⇒l⊥m
②α⊥β⇒l∥m
③l∥m⇒α⊥β
④l⊥m⇒α⊥β
其中正确的两个命题是( )
①α∥β⇒l⊥m
②α⊥β⇒l∥m
③l∥m⇒α⊥β
④l⊥m⇒α⊥β
其中正确的两个命题是( )
| A、①与② | B、③与④ |
| C、②与④ | D、①与③ |
lg2+lg50=( )
| A、1 | B、2 | C、3 | D、4 |
设集合A={x||x|-1=0},B={x|x2-a≤0},则“a=4”是“A∪B=B”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不必要也不充分条件 |
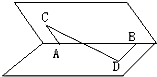 如图,在锐二面角α-AB-β内,AC?β,BD?α,AC⊥AB于A,BD⊥AB于B,且AC=BD=2,AB=4,CD=
如图,在锐二面角α-AB-β内,AC?β,BD?α,AC⊥AB于A,BD⊥AB于B,且AC=BD=2,AB=4,CD=