题目内容
已知曲线f(x)=3mx+sinx上存在相互垂直的两条切线,则实数m的值为 .
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:先求导函数,函数f(x)的图象上存在互相垂直的切线,不妨设在x=k与x=n处的切线互相垂直则(3m+cosk)(3m+cosn)=-1,然后整理,根据m的值必然存在,△≥0可求出m的值.
解答:
解:∵f(x)=3mx+sinx,
∴f′(x)=3m+cosx,
函数f(x)=3mx+sinx的图象上存在互相垂直的切线,
不妨设在x=k与x=n处的切线互相垂直,
则(3m+cosk)(3m+cosn)=-1
∴9m2+3(cosk+cosn)m+(coskcosn+1)=0 (*)
因为m的值必然存在,即方程(*)必然有解,所以
判别式△=9(cosk+cosn)2-36(coskcosn+1)≥0
所以 cos2k+cos2n-2coskcosn=(cosk-cosn)2≥4
解得cosk-cosn≥2 或 cosk-cosn≤-2
由于|cosx|≤1,所以有cosk=1,cosn=-1 或 cosk=-1,cosn=1,且△=0
所以(*)变为:m2=0所以m=0
故答案为:0
∴f′(x)=3m+cosx,
函数f(x)=3mx+sinx的图象上存在互相垂直的切线,
不妨设在x=k与x=n处的切线互相垂直,
则(3m+cosk)(3m+cosn)=-1
∴9m2+3(cosk+cosn)m+(coskcosn+1)=0 (*)
因为m的值必然存在,即方程(*)必然有解,所以
判别式△=9(cosk+cosn)2-36(coskcosn+1)≥0
所以 cos2k+cos2n-2coskcosn=(cosk-cosn)2≥4
解得cosk-cosn≥2 或 cosk-cosn≤-2
由于|cosx|≤1,所以有cosk=1,cosn=-1 或 cosk=-1,cosn=1,且△=0
所以(*)变为:m2=0所以m=0
故答案为:0
点评:本题主要考查了导数的几何意义,以及判别式判定方程的根,同时考查了函数与方程的思想和计算能力,属于中档题.

练习册系列答案
相关题目
已知集合P={x,y,z},Q={1,2},映射f:P→Q中满足f(y)=2的映射的个数共有( )
| A、2 | B、4 | C、5 | D、6 |
函数y=x|x|的图象大致是( )
A、 |
B、 |
C、 |
D、 |
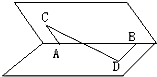 如图,在锐二面角α-AB-β内,AC?β,BD?α,AC⊥AB于A,BD⊥AB于B,且AC=BD=2,AB=4,CD=
如图,在锐二面角α-AB-β内,AC?β,BD?α,AC⊥AB于A,BD⊥AB于B,且AC=BD=2,AB=4,CD=