题目内容
设函数f(x)=ex-1+
(a∈R).
(1)若函数f(x)在x=1处有极值,求a的值;
(2)在(1)条件下,若函数g(x)=f(x)+b在(0,+∞)上有零点,求b的最大值;
(3)若f(x)在(1,2)上为单调函数,求实数a的取值范围.
| a |
| x |
(1)若函数f(x)在x=1处有极值,求a的值;
(2)在(1)条件下,若函数g(x)=f(x)+b在(0,+∞)上有零点,求b的最大值;
(3)若f(x)在(1,2)上为单调函数,求实数a的取值范围.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的概念及应用,导数的综合应用
分析:(1)利用极值点处的导数为零列方程求a,但勿忘验证;
(2)先利用导数研究函数的单调性、极值,最后利用极值的符号,端点处函数值的符号结合图象来求解;
(3)即该函数在(1,2)上导数恒为正或恒为负,最终转化为不等式恒成立问题.
(2)先利用导数研究函数的单调性、极值,最后利用极值的符号,端点处函数值的符号结合图象来求解;
(3)即该函数在(1,2)上导数恒为正或恒为负,最终转化为不等式恒成立问题.
解答:
解:(Ⅰ)f'(x)=ex-1-
,又函数f(x)在x=1处有极值,
∴f'(1)=0,a=1,经检验符合题意.
(2)g'(x)=ex-1-
,
当x∈(0,1)时,g'(x)<0,g(x)为减函数,
当x=1时,g'(x)=0,
当x∈(1,+∞)时g'(x)>0,g(x)为增函数,
∴g(x)在x=1时取得极小值g(1)=2+b,
依题意g(1)≤0,∴b≤-2,∴b的最大值为-2;
(3)f'(x)=ex-1-
,当f (x)在(1,2)上单调递增时,ex-1-
≥0在[1,2]上恒成立,
∴a≤x2ex-1,令h(x)=x2ex-1,则h'(x)=ex-1( x2+2 x)>0在[1,2]上恒成立,即h(x) 在[1,2]上单调递增,
∴h(x) 在[1,2]上的最小值为h(1)=1,∴a≤1;
当f(x)在[1,2]上单调递减时,同理a≥x2ex-1,
h(x)=x2ex-1在[1,2]上的最大值为h(2)=4e,∴a≥4e;
综上,实数a的取值范围为a≤1或a≥4e;
| a |
| x2 |
∴f'(1)=0,a=1,经检验符合题意.
(2)g'(x)=ex-1-
| 1 |
| x2 |
当x∈(0,1)时,g'(x)<0,g(x)为减函数,
当x=1时,g'(x)=0,
当x∈(1,+∞)时g'(x)>0,g(x)为增函数,
∴g(x)在x=1时取得极小值g(1)=2+b,
依题意g(1)≤0,∴b≤-2,∴b的最大值为-2;
(3)f'(x)=ex-1-
| a |
| x2 |
| a |
| x2 |
∴a≤x2ex-1,令h(x)=x2ex-1,则h'(x)=ex-1( x2+2 x)>0在[1,2]上恒成立,即h(x) 在[1,2]上单调递增,
∴h(x) 在[1,2]上的最小值为h(1)=1,∴a≤1;
当f(x)在[1,2]上单调递减时,同理a≥x2ex-1,
h(x)=x2ex-1在[1,2]上的最大值为h(2)=4e,∴a≥4e;
综上,实数a的取值范围为a≤1或a≥4e;
点评:强调第一点,利用极值点处函数值求字母要验证,第二点,要准确理解单调函数的概念,同时此类问题要转化为不等式恒成立,转化为函数的最值问题作为落脚点.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
已知椭圆
+
=1上的一点M到焦点F1的距离为2,N是MF1的中点,O为原点,则|ON|等于( )
| x2 |
| 25 |
| y2 |
| 9 |
| A、2 | ||
| B、4 | ||
| C、8 | ||
D、
|
a,b是异面直线,点P∉a∪b,下列命题:
(1)过P可作平面与a,b均平行;
(2)过P可作直线与a,b都相交;
(3)过P可作平面与a,b都垂直;
(4)过P可作直线a,b都垂直,
其中真命题的个数是( )
(1)过P可作平面与a,b均平行;
(2)过P可作直线与a,b都相交;
(3)过P可作平面与a,b都垂直;
(4)过P可作直线a,b都垂直,
其中真命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
已知函数f(x)=-x3+bx2-
b3(b>0),有且仅有两个不同的零点x1,x2,则( )
| 4 |
| 27 |
| A、x1+x2>0,x1x2<0 |
| B、x1+x2>0,x1x2>0 |
| C、x1+x2<0,x1x2<0 |
| D、x1+x2<0,x1x2>0 |
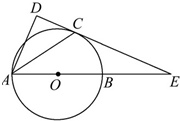 如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.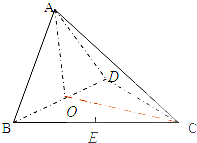 如图,在三棱锥A-BCD中,AO⊥平面BCD;O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=
如图,在三棱锥A-BCD中,AO⊥平面BCD;O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=