题目内容
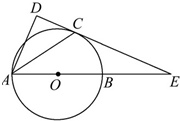 如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.(1)求证:直线CD为⊙O的切线;
(2)当AB=2BE,且CE=
| 3 |
考点:与圆有关的比例线段,圆的切线的判定定理的证明
专题:立体几何
分析:(1)连接OC,由已知条件推导出OC∥AD,又CD⊥AD,从而CD⊥OC,由此能证明CD为⊙O的切线.
(2)由已知得OE=2OC,在Rt△EOC中,设CO=x,即OE=2x,由勾股定理得:CE=
x,由此能求出AD.
(2)由已知得OE=2OC,在Rt△EOC中,设CO=x,即OE=2x,由勾股定理得:CE=
| 3 |
解答:
(1)证明:连接OC,
∵AC平分∠DAB,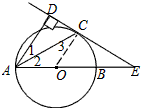 ∴∠1=∠2,
∴∠1=∠2,
∵又AO=CO,∴∠3=∠2,∴∠1=∠3,
∴OC∥AD,∵又CD⊥AD,∴CD⊥OC,
∴CD为⊙O的切线;
(2)解:∵直径AB=2BE,
∴OE=2OC,
在Rt△EOC中,设CO=x,即OE=2x,
由勾股定理得:CE=
x,
又∵CE=
,∴x=1,即OC=1,
∵OC∥AD,∴△EOC∽△EAD,
∴
=
,即
=
,
解得AD=
.
∵AC平分∠DAB,
 ∴∠1=∠2,
∴∠1=∠2,∵又AO=CO,∴∠3=∠2,∴∠1=∠3,
∴OC∥AD,∵又CD⊥AD,∴CD⊥OC,
∴CD为⊙O的切线;
(2)解:∵直径AB=2BE,
∴OE=2OC,
在Rt△EOC中,设CO=x,即OE=2x,
由勾股定理得:CE=
| 3 |
又∵CE=
| 3 |
∵OC∥AD,∴△EOC∽△EAD,
∴
| OC |
| AD |
| OE |
| AE |
| 1 |
| AD |
| 2 |
| 3 |
解得AD=
| 3 |
| 2 |
点评:本题考查直线是圆的切线的证明,考查线段长的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
某公司员工义务献血,在体检合格人中,O型血有10人,A型血有5人,B型血有8人,AB型血有3人,从4种血型的人中各选一人去献血,不同的选法种数为( )
| A、1200 | B、600 |
| C、300 | D、26 |
已知实数1,m,9成等比数列,则圆锥曲线
+y2=1的离心率为( )
| x2 |
| m |
| A、A、 | B、B、 | C、C、 | D、D、 |