题目内容
13.已知圆Г过点(1,1)、(1,3)、(2,2),P是圆Г的一个动点,若A(-3,4),O为坐标原点,则$\overrightarrow{OP}$•$\overrightarrow{OA}$的最大值为( )| A. | 0 | B. | 4 | C. | 12 | D. | 10 |
分析 先求出圆的标准方程,设P的坐标为(x,y),根据向量的坐标的运算得到$\overrightarrow{OP}$•$\overrightarrow{OA}$=-3x+4y,设-3x+4y=t,即3x-4y+t=0,当直线与圆相切时有最大值.
根据点到直线距离公式即可求出.
解答 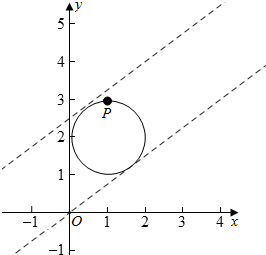 解:设圆的标准方程为(x-a)2+(y-b)2=r2,
解:设圆的标准方程为(x-a)2+(y-b)2=r2,
则$\left\{\begin{array}{l}{(1-a)^{2}+(1-b)^{2}={r}^{2}}\\{(1-a)^{2}+(3-b)^{2}={r}^{2}}\\{(2-a)^{2}+(2-b)^{2}={r}^{2}}\end{array}\right.$,
解得a=1,b=2,r=1,
∴(x-1)2+(y-2)2=1,
设P的坐标为(x,y),
∵A(-3,4),O为坐标原点,
∴$\overrightarrow{OP}$•$\overrightarrow{OA}$=-3x+4y,
设-3x+4y=t,即3x-4y+t=0,
则y=$\frac{3}{4}$x+$\frac{t}{4}$
当直线3x-4y+t=0与圆相切时,t的值最大,
∴d=$\frac{|1×3-2×4+t|}{\sqrt{{3}^{2}+{4}^{2}}}$=1,
即|t-5|=5,
解得t=0,或t=10,
∴t的最大值为10.
∴t的最大值为10.
故选:D.
点评 本题考查了直线和圆的位置关系,圆的方程的解法和向量的坐标运算,属于中档题.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
1.下列函数中,在(-∞,0)上单调递增的是( )
| A. | y=|x| | B. | y=log2|x| | C. | $y={|x|^{\frac{1}{2}}}$ | D. | y=0.5|x| |
3.小明每天步行上学,途中要走过几条街道,假设街道之间是平行或垂直的,小明走出家门口直行50米后右转直行50米,之后左转直行100米后再右转直行100米到达学校,则小明家与学校的直线距离是( )
| A. | 100$\sqrt{2}$米 | B. | 120$\sqrt{2}$米 | C. | 150$\sqrt{3}$米 | D. | 150$\sqrt{2}$米 |