题目内容
18.己知集合A={x|log2(a-x)≤2},集合B={x|x2-3x+2=0}.(1)若A∩B=B,求实数a的取值范围;
(2)若A∩B=∅,求实数a的取值范围.
分析 (1)若A∩B=B,B⊆A,可得log2(a-1)≤2且log2(a-2)≤2,求实数a的取值范围;
(2)若A∩B=∅,可得log2(a-1)>2且log2(a-2)>2,即可求实数a的取值范围.
解答 解:(1)B={1,2},
∵A∩B=B,
∴B⊆A,
∴log2(a-1)≤2且log2(a-2)≤2,
∴2<a≤5;
(2)∵A∩B=∅,
∴log2(a-1)>2且log2(a-2)>2,
∴a>6.
点评 本题考查集合的关系,考查学生解不等式的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.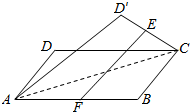 设E,F分别是正方形ABCD中CD、AB边的中点,将△ADC沿对角线AC对折,使得直线EF与AC异面,记直线EF与平面ABC所成角为α,与异面直线AC所成角为β,则当tanβ=$\frac{1}{2}$时,tanα=( )
设E,F分别是正方形ABCD中CD、AB边的中点,将△ADC沿对角线AC对折,使得直线EF与AC异面,记直线EF与平面ABC所成角为α,与异面直线AC所成角为β,则当tanβ=$\frac{1}{2}$时,tanα=( )
 设E,F分别是正方形ABCD中CD、AB边的中点,将△ADC沿对角线AC对折,使得直线EF与AC异面,记直线EF与平面ABC所成角为α,与异面直线AC所成角为β,则当tanβ=$\frac{1}{2}$时,tanα=( )
设E,F分别是正方形ABCD中CD、AB边的中点,将△ADC沿对角线AC对折,使得直线EF与AC异面,记直线EF与平面ABC所成角为α,与异面直线AC所成角为β,则当tanβ=$\frac{1}{2}$时,tanα=( )| A. | $\frac{3\sqrt{5}}{16}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{51}}{17}$ | D. | $\frac{\sqrt{57}}{19}$ |
6.若sinα≥$\sqrt{3}$cosα,α∈[0,2π],则α的取值范围是( )
| A. | [$\frac{π}{3}$,$\frac{π}{2}$] | B. | [$\frac{π}{3}$,$\frac{4π}{3}$] | C. | [$\frac{π}{3}$,π] | D. | [0,π] |
3.小明每天步行上学,途中要走过几条街道,假设街道之间是平行或垂直的,小明走出家门口直行50米后右转直行50米,之后左转直行100米后再右转直行100米到达学校,则小明家与学校的直线距离是( )
| A. | 100$\sqrt{2}$米 | B. | 120$\sqrt{2}$米 | C. | 150$\sqrt{3}$米 | D. | 150$\sqrt{2}$米 |
10.在梯形ABCD中,AB∥CD,$\overrightarrow{AB}$=2$\overrightarrow{DC}$,$\overrightarrow{BE}$=$\overrightarrow{EC}$,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则向量$\overrightarrow{AE}$等于( )
| A. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | B. | $\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | C. | $\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ |
8.已知a2≤1,|b|≤1,则满足函数y=log3(x2+2ax+b)的定义域为全体实数R的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
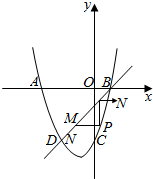 如图,抛物线y=ax2+2x-6与X轴交于点A(-6,0),B(点A在点B的左侧),与y轴交于点C,直线BD与抛物线交于点D,点D与点C关于该抛物线的对称轴对称.
如图,抛物线y=ax2+2x-6与X轴交于点A(-6,0),B(点A在点B的左侧),与y轴交于点C,直线BD与抛物线交于点D,点D与点C关于该抛物线的对称轴对称.