题目内容

16．如图示中的幂函数在第一象限的图象，则下面四个选项中正确的是（　　）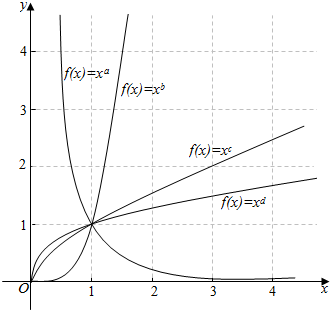
A．a+b+c+d为正数B．b+c+d-a可能为零
C．a-b-c-d为负数D．b×c×d×a符号不能确定

分析 根据幂函数y=xn的性质，在第一象限内的图象，当n＞0时，函数是增函数，n越大，递增速度越快；当n＜0时，函数是减函数，|n|越大，曲线越陡峭，由此能求出结果．

解答 解：由幂函数在第一象限的图象，得：
在第一象限，f（x）=xa是减函数，∴a＜0，
在第一象限，f（x）=xb，f（x）=xc，f（x）=xd都是增函数，
根据幂函数y=xn的性质，在第一象限内的图象
当n＞0时，n越大，递增速度越快，
当n＜0时，|n|越大，曲线越陡峭，
∴b＞c＞d＞0，
∴a+b+c+d符号不能确定，故A错误；
b+c+d-a一定大于0，故B错误；
a-b-c-d＜0，故C正确；
b×c×d×a＜0，故D错误．
故选：C．

点评 本题考查命题真假的判断，是基础题，解题时要认真审题，注意幂函数的图象的性质的合理运用．

练习册系列答案
相关题目
10．已知命题p：{x||x-1|＜c（c＞0）}，命题q：{x||x-3|＞4}，且￢p是q成立的充分且不必要条件，求实数c的取值范围．
7．已知函数f（x）=x2+alnx．
（Ⅰ）当a=-2时，求函数f（x）的单调区间和极值；
（Ⅱ）若g（x）=f（x）+$\frac{2}{x}$在[1，+∞）上是单调增函数，求实数a的取值范围．
4．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的右顶点、左焦点分别为A、F，点B（0，-b），若|$\overrightarrow{BA}+\overrightarrow{BF}|=|\overrightarrow{BA}-\overrightarrow{BF|}$，则双曲线的离心率值为$\frac{{\sqrt{5}+1}}{2}$．
11．对于函数f（x），若存在常数a≠0，使得x取定义域内的每一个值，都有f（x）=-f（2a-x），则称f（x）为“准奇函数”．给定下列函数：①f（x）=$\frac{1}{x+1}$，②f（x）=（x+1）2；③f（x）=x3；④f（x）=sin（x+1），其中的“准奇函数”是①④（写出所有“准奇函数”的序号）
1．下列函数中，在（-∞，0）上单调递增的是（　　）
A．y=|x|B．y=log2|x|C．$y={|x|^{\frac{1}{2}}}$D．y=0.5|x|
8．已知数列{an}中，a1=a（0＜a≤2），an+1=$\left\{\begin{array}{l}{a_n}-2，（{a_n}＞2）\\-{a_n}+3，（{a_n}≤2）\end{array}$（n∈N*），记Sn=a1+a2+…+an，若Sn=2015，则n=1343．
5．△ABC中，角A、B、C所对的边分别为a、b、c，a＞b且sin2B+sin2C=tan$\frac{A}{2}$（cos2B+cos2C）．
（I）求角A的大小；
（Ⅱ）若a=4，求b+c的取值范围．
6．若sinα≥$\sqrt{3}$cosα，α∈[0，2π]，则α的取值范围是（　　）
A．[$\frac{π}{3}$，$\frac{π}{2}$]B．[$\frac{π}{3}$，$\frac{4π}{3}$]C．[$\frac{π}{3}$，π]D．[0，π]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网