题目内容
已知实数a＞0，b＜0，方程x2-ax+b=0在区间（-1，1）上恰有一根，求
的取值范围．
| a+1 |
| b+1 |
考点：一元二次方程的根的分布与系数的关系
专题：计算题,函数的性质及应用,不等式的解法及应用
分析：方程x2-ax+b=0在区间（-1，1）上恰有一根，令f（x）=x2-ax+b，运用零点存在定理可得f（-1）f（1）＜0，在平面直角坐标系中，画出可行域，再由
=
表示点P（-1，-1）和（b，a）两点的斜率，通过图象观察即可得到范围．
| a+1 |
| b+1 |
| a-(-1) |
| b-(-1) |
解答：
解：由于实数a＞0，b＜0，
方程x2-ax+b=0在区间（-1，1）上恰有一根，
令f（x）=x2-ax+b，则f（-1）f（1）＜0，
即为（1-a+b）（1+a+b）＜0，
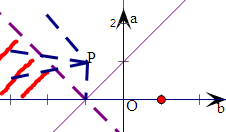
作出不等式（1-a+b）（1+a+b）＜0且a＞0，b＜0的点（b，a）
表示的平面区域，
由于
=
表示点P（-1，-1）和（b，a）两点的斜率，
由可行域可得，两点的斜率范围是（-1，0]∪（0，+∞）=（-1，+∞）．
即有
的取值范围为（-1，+∞）．
解：由于实数a＞0，b＜0，方程x2-ax+b=0在区间（-1，1）上恰有一根，
令f（x）=x2-ax+b，则f（-1）f（1）＜0，
即为（1-a+b）（1+a+b）＜0，
作出不等式（1-a+b）（1+a+b）＜0且a＞0，b＜0的点（b，a）
表示的平面区域，
由于
| a+1 |
| b+1 |
| a-(-1) |
| b-(-1) |
由可行域可得，两点的斜率范围是（-1，0]∪（0，+∞）=（-1，+∞）．
即有
| a+1 |
| b+1 |
点评：本题考查二次方程的实根的分布，主要考查函数的零点存在定理的运用，运用不等式表示的平面区域，借助直线的斜率公式是解题的关键．
练习册系列答案
相关题目
若（x+
）4=a0+a1x+a2x2+a3x3+a4x4，则（a0+a2+a4）2-（a1+a3）2的值为（ ）
| 3 |
| A、-16 | ||
| B、16 | ||
C、
| ||
D、
|
已知等比数列{an}的公比q≠1，则下面说法中不正确的是（ ）
| A、{an+2+an}是等比数列 |
| B、对于k∈N*，k＞1，ak-1+ak+1≠2ak |
| C、对于n∈N*，都有anan+2＞0 |
| D、若a2＞a1，则对于任意n∈N*，都有an+1＞an |