题目内容
某公司生产产品A,产品质量按测试指标分为:指标大于或等于90为一等品,大于或等于80小于90为二等品,小于80为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利30元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
根据上表统计得到甲、乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率.
(1)计算甲生产一件产品A,给工厂带来盈利不小于30元的概率;
(2)若甲一天能生产20件产品A,乙一天能生产15件产品A,估计甲乙两人一天生产的35件产品A中三等品的件数.
| 测试指标 | [70,75] | [75,80) | [80,85) | [85,90) | [90,95) | [95,100) |
| 甲 | 3 | 7 | 20 | 40 | 20 | 10 |
| 乙 | 5 | 15 | 35 | 35 | 7 | 3 |
(1)计算甲生产一件产品A,给工厂带来盈利不小于30元的概率;
(2)若甲一天能生产20件产品A,乙一天能生产15件产品A,估计甲乙两人一天生产的35件产品A中三等品的件数.
考点:分层抽样方法,古典概型及其概率计算公式
专题:概率与统计
分析:(1)根据古典概型的概率公式进行求解即可.
(2)根据条件求出甲乙两人一天内生产的三等品的件数即可得到结论.
(2)根据条件求出甲乙两人一天内生产的三等品的件数即可得到结论.
解答:
解:(1)甲生产一件产品A,三等品的件数为3+7=10,此时给工厂带来盈利小于30元的概率为
=
,
则给工厂带来盈利不小于30元的概率为P=1-
=
.
(2)估计甲一天生产的20件产品A中有20×
=2件三等品,
估计乙一天生产的15件产品A中有15×
=3件三等品,
所以估计甲乙两人一天生产的35件产品A中共有5件三等品.
| 10 |
| 100 |
| 1 |
| 10 |
则给工厂带来盈利不小于30元的概率为P=1-
| 1 |
| 10 |
| 9 |
| 10 |
(2)估计甲一天生产的20件产品A中有20×
| 1 |
| 10 |
估计乙一天生产的15件产品A中有15×
| 2 |
| 10 |
所以估计甲乙两人一天生产的35件产品A中共有5件三等品.
点评:本题主要考查统计与概率的应用,比较基础.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
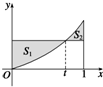 在区间[0,1]上给定曲线y=x2,试在此区间内确定点t的值,使图中阴影部分的面积:
在区间[0,1]上给定曲线y=x2,试在此区间内确定点t的值,使图中阴影部分的面积: