题目内容
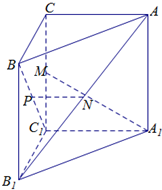 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=| 6 |
(1)求证:PN∥平面ABC;
(2)求证:A1M⊥AB1C1;
(3)求点M到平面AA1B1的距离.
考点:点、线、面间的距离计算,直线与平面平行的判定,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)证明PN∥平面ABC,利用线面平行的判定,只需证明PN∥AC;
(2)证明A1M⊥AB1C1,只需证明AC1⊥A1M,B1C1⊥A1M;
(3)利用VM-AA1B1=VB1-MAA1,可求点M到平面AA1B1的距离,
(2)证明A1M⊥AB1C1,只需证明AC1⊥A1M,B1C1⊥A1M;
(3)利用VM-AA1B1=VB1-MAA1,可求点M到平面AA1B1的距离,
解答:
 (1)证明:连结CB1,
(1)证明:连结CB1,
∵P是BC1的中点,∴CB1过点P,--(1分)
∵N为AB1的中点,∴PN∥AC,---------------------------(2分)
∵AC?面ABC,PN?面ABC,
∴PN∥平面ABC.--------------------------------------(4分)
(2)证法一:连结AC1,在直角△ABC中,
∵BC=1,∠BAC=30°,
∴AC=A1C1=
-----------------------------------(5分)
∵
=
=
,
∴Rt△A1C1M~Rt△C1CA--------------------------------------------------------(7分)
∴∠A1MC1=∠CAC1,∴∠AC1C+∠CAC1=∠AC1C+∠A1MC1=90°
∴AC1⊥A1M.-------------------------------------------------------------------(8分)
∵B1C1⊥C1A1,CC1⊥B1C1,且C1A1∩CC1=C1
∴B1C1⊥平面AA1CC1,-----------------------------------------------------------(9分)
∴B1C1⊥A1M,又AC1∩B1C1=C1,故A1M⊥平面A B1C1,-------------------------(11分)
证法二:连结AC1,在直角△ABC中,∵BC=1,∠BAC=30°,
∴AC=A1C1=
-------------------------------------------------------------(5分)
设∠AC1A1=α,∠MA1C1=β
∵tanαtanβ=
•
=
•
=1,------------------------------------------(7分)
∴α+β=90° 即AC1⊥A1M.-------------------------------------------------------(8分)
∵B1C1⊥C1A1,CC1⊥B1C1,且C1A1∩CC1=C1
∴B1C1⊥平面AA1CC1,-----------------------------------------------------------(9分)
∴B1C1⊥A1M,又AC1∩B1C1=C1
故A1M⊥面A B1C1,------------------------------------------------------------(11分)】
(3)设点M到平面AA1B1的距离为h,
由(2)知B1C1⊥平面AA1CC1
∵VM-AA1B1=VB1-MAA1------------------------------------------------------------(12分)
∴S△AA1B1•h=S△MAA1•B1C1
∴h=
=
=
.
即点M到平面AA1B1的距离为
.----------------------------------------------(14分)
 (1)证明:连结CB1,
(1)证明:连结CB1,∵P是BC1的中点,∴CB1过点P,--(1分)
∵N为AB1的中点,∴PN∥AC,---------------------------(2分)
∵AC?面ABC,PN?面ABC,
∴PN∥平面ABC.--------------------------------------(4分)
(2)证法一:连结AC1,在直角△ABC中,
∵BC=1,∠BAC=30°,
∴AC=A1C1=
| 3 |
∵
| CC1 |
| A1C1 |
| A1C1 |
| MC1 |
| 2 |
∴Rt△A1C1M~Rt△C1CA--------------------------------------------------------(7分)
∴∠A1MC1=∠CAC1,∴∠AC1C+∠CAC1=∠AC1C+∠A1MC1=90°
∴AC1⊥A1M.-------------------------------------------------------------------(8分)
∵B1C1⊥C1A1,CC1⊥B1C1,且C1A1∩CC1=C1
∴B1C1⊥平面AA1CC1,-----------------------------------------------------------(9分)
∴B1C1⊥A1M,又AC1∩B1C1=C1,故A1M⊥平面A B1C1,-------------------------(11分)
证法二:连结AC1,在直角△ABC中,∵BC=1,∠BAC=30°,
∴AC=A1C1=
| 3 |
设∠AC1A1=α,∠MA1C1=β
∵tanαtanβ=
| AA1 |
| A1C1 |
| MC1 |
| A1C1 |
| ||
|
| ||
| 2 |
∴α+β=90° 即AC1⊥A1M.-------------------------------------------------------(8分)
∵B1C1⊥C1A1,CC1⊥B1C1,且C1A1∩CC1=C1
∴B1C1⊥平面AA1CC1,-----------------------------------------------------------(9分)
∴B1C1⊥A1M,又AC1∩B1C1=C1
故A1M⊥面A B1C1,------------------------------------------------------------(11分)】
(3)设点M到平面AA1B1的距离为h,
由(2)知B1C1⊥平面AA1CC1
∵VM-AA1B1=VB1-MAA1------------------------------------------------------------(12分)
∴S△AA1B1•h=S△MAA1•B1C1
∴h=
| S△MAA1•B1C1 |
| S△AA1B1 |
| ||||||
|
| ||
| 2 |
即点M到平面AA1B1的距离为
| ||
| 2 |
点评:本题考查直线与平面平行的证明,考查直线与平面垂直的证明,考查点M到平面AA1B1的距离,用好等体积是关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 2013年4月20日8点02分四川省雅安市芦山县(北纬30.3度,东经103.0度)
2013年4月20日8点02分四川省雅安市芦山县(北纬30.3度,东经103.0度)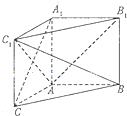 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,且AB=AC=AA1=1.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,且AB=AC=AA1=1.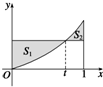 在区间[0,1]上给定曲线y=x2,试在此区间内确定点t的值,使图中阴影部分的面积:
在区间[0,1]上给定曲线y=x2,试在此区间内确定点t的值,使图中阴影部分的面积: