题目内容
化简求值:
(1)
;
(2)已知cos(α-
)=-
,sin(
-β)=
,且
<α<π,0<β<
,求cos
的值.
(1)
| 2cos10°-sin20° |
| cos20° |
(2)已知cos(α-
| β |
| 2 |
| 1 |
| 9 |
| α |
| 2 |
| 2 |
| 3 |
| π |
| 2 |
| π |
| 2 |
| α+β |
| 2 |
考点:两角和与差的余弦函数,三角函数的化简求值
专题:三角函数的图像与性质
分析:(1)利用cos10°=sin80°=sin(60°+20°),利用两角和的正弦公式展开,合并即可.
(2)求出α-
的正弦函数值,
-β的余弦函数值,然后利用
=(α-
)-(
-β)通过两角和与差的三角函数求解所求表达式的值即可.
(2)求出α-
| β |
| 2 |
| α |
| 2 |
| α+β |
| 2 |
| β |
| 2 |
| α |
| 2 |
解答:
解:(1)∵2cos10°=2sin80°
=2sin(60°+20°)
=2(
cos20°+
sin20°)
=
cos20°+sin20°,
∴
=
=
.
(2)cos(α-
)=-
,sin(
-β)=
,且
<α<π,0<β<
,
∴α-
∈(
,π),∴sin(α-
)=
=
.
-β∈(-
,
),cos(
-β)=
=
.
∴cos
=cos[(α-
)-(
-β)]=cos(α-
)cos(
-β)+sin(α-
)sin(
-β)
=-
×
+
×
=
.
=2sin(60°+20°)
=2(
| ||
| 2 |
| 1 |
| 2 |
=
| 3 |
∴
| 2cos10°-sin20° |
| cos20° |
| ||
| cos20° |
| 3 |
(2)cos(α-
| β |
| 2 |
| 1 |
| 9 |
| α |
| 2 |
| 2 |
| 3 |
| π |
| 2 |
| π |
| 2 |
∴α-
| β |
| 2 |
| π |
| 4 |
| β |
| 2 |
1-(-
|
4
| ||
| 9 |
| α |
| 2 |
| π |
| 4 |
| π |
| 4 |
| α |
| 2 |
1-(
|
| ||
| 3 |
∴cos
| α+β |
| 2 |
| β |
| 2 |
| α |
| 2 |
| β |
| 2 |
| α |
| 2 |
| β |
| 2 |
| α |
| 2 |
=-
| 1 |
| 9 |
| ||
| 3 |
| 2 |
| 3 |
4
| ||
| 9 |
=
7
| ||
| 27 |
点评:本题考查三角函数的化简求值,两角和与差的三角函数,角的变换,以及“2cos10°=2sin80°=2sin(60°+20°)”的思考与转化,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设全集U={3,4,5,6},集合A={3,5,6},B={4,5,6},则∁UA∩B=( )
| A、{4,7} | B、{3,6} |
| C、{4} | D、{7} |
 2013年4月20日8点02分四川省雅安市芦山县(北纬30.3度,东经103.0度)
2013年4月20日8点02分四川省雅安市芦山县(北纬30.3度,东经103.0度)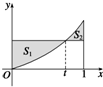 在区间[0,1]上给定曲线y=x2,试在此区间内确定点t的值,使图中阴影部分的面积:
在区间[0,1]上给定曲线y=x2,试在此区间内确定点t的值,使图中阴影部分的面积: