题目内容
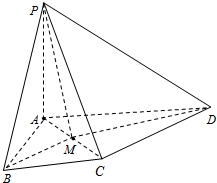 如图所示,PA⊥平面ABCD,△ABC为等边三角形,AP=AB,AC⊥CD,M为AC的中点.
如图所示,PA⊥平面ABCD,△ABC为等边三角形,AP=AB,AC⊥CD,M为AC的中点. (Ⅰ)求证:BM∥平面PCD;
(Ⅱ)若直线PD与平面PAC所成角的正切值为
| ||
| 2 |
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:空间角
分析:(Ⅰ)由已知条件推导出BM⊥AC,从而得到BM∥CD,由此能够证明BM∥平面PCD.
(Ⅱ)由已知条件推导出PA⊥CD,从而得到CD⊥平面PAC.所以直线PD与平面PAC所成角为∠DPC,在平面PAD中,过N作NH⊥PD,连结MH,由题意得∠MHN为二面角A-PD-M的平面角,由此能求出二面角A-PD-M的正切值.
(Ⅱ)由已知条件推导出PA⊥CD,从而得到CD⊥平面PAC.所以直线PD与平面PAC所成角为∠DPC,在平面PAD中,过N作NH⊥PD,连结MH,由题意得∠MHN为二面角A-PD-M的平面角,由此能求出二面角A-PD-M的正切值.
解答:
(本题满分14分)
(Ⅰ)证明:∵△ABC为等边三角形,M为AC的中点,
∴BM⊥AC.又∵AC⊥CD,∴在平面ABCD中,有BM∥CD.…(3分)
又∵CD?平面PCD,BM?平面PCD,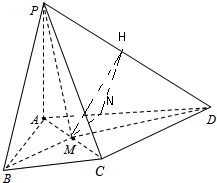
∴BM∥平面PCD.…(5分)
(Ⅱ)解:∵PA⊥平面ABCD,CD?平面ABCD,
∴PA⊥CD,又∵AC⊥CD,PA∩AC=A,
∴CD⊥平面PAC.
∴直线PD与平面PAC所成角为∠DPC.…(7分)
在Rt△PCD中,tan∠DPC=
=
.
设AP=AB=a,则AC=a,PC=
a,
∴CD=
PC=
a,
在Rt△ACD中,AD2=AC2+CD2=4a2,∴AD=2a.…(9分)
∵PA⊥平面ABCD,∴平面PAD⊥平面ABCD.
在Rt△ACD中,过M作MN⊥AD.
又∵平面ABCD∩平面PAD=AD,MN?平面ABCD,
∴MN⊥平面PAD.
在平面PAD中,过N作NH⊥PD,连结MH,
则PD⊥平面MNH.
∴∠MHN为二面角A-PD-M的平面角.…(12分)
在Rt△ACD中,MN=
a,AN=
a,ND=
a,
∴
=
,∴NH=
=
a,
∴tan∠MHN=
=
=
,
∴二面角A-PD-M的正切值为
.…(14分)
(Ⅰ)证明:∵△ABC为等边三角形,M为AC的中点,
∴BM⊥AC.又∵AC⊥CD,∴在平面ABCD中,有BM∥CD.…(3分)
又∵CD?平面PCD,BM?平面PCD,

∴BM∥平面PCD.…(5分)
(Ⅱ)解:∵PA⊥平面ABCD,CD?平面ABCD,
∴PA⊥CD,又∵AC⊥CD,PA∩AC=A,
∴CD⊥平面PAC.
∴直线PD与平面PAC所成角为∠DPC.…(7分)
在Rt△PCD中,tan∠DPC=
| CD |
| PC |
| ||
| 2 |
设AP=AB=a,则AC=a,PC=
| 2 |
∴CD=
| ||
| 2 |
| 3 |
在Rt△ACD中,AD2=AC2+CD2=4a2,∴AD=2a.…(9分)
∵PA⊥平面ABCD,∴平面PAD⊥平面ABCD.
在Rt△ACD中,过M作MN⊥AD.
又∵平面ABCD∩平面PAD=AD,MN?平面ABCD,
∴MN⊥平面PAD.
在平面PAD中,过N作NH⊥PD,连结MH,
则PD⊥平面MNH.
∴∠MHN为二面角A-PD-M的平面角.…(12分)
在Rt△ACD中,MN=
| ||
| 4 |
| 1 |
| 4 |
| 7 |
| 4 |
∴
| NH |
| PA |
| DN |
| PD |
| PA•DN |
| PD |
| 7 | ||
4
|
∴tan∠MHN=
| MN |
| NH |
| ||||
|
| ||
| 7 |
∴二面角A-PD-M的正切值为
| ||
| 7 |
点评:本题考查直线与平面平行的证明,考查二面角的正切值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
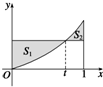 在区间[0,1]上给定曲线y=x2,试在此区间内确定点t的值,使图中阴影部分的面积:
在区间[0,1]上给定曲线y=x2,试在此区间内确定点t的值,使图中阴影部分的面积: