题目内容
已知函数f(x)=2x-1的反函数为y=f-1(x),记g(x)=f-1(x-1)
(1)求函数y=2f-1(x)-g(x)的最小值;
(2)集合A={x|[1+f(x)]•|f(x)|≥2},对于任意的x∈A,不等式2f-1(x+m)-g(x)≥0恒成立,求实数m的取值范围.
(1)求函数y=2f-1(x)-g(x)的最小值;
(2)集合A={x|[1+f(x)]•|f(x)|≥2},对于任意的x∈A,不等式2f-1(x+m)-g(x)≥0恒成立,求实数m的取值范围.
考点:函数恒成立问题
专题:转化思想,函数的性质及应用
分析:(1)求出原函数的反函数,然后推出函数y=2f-1(x)-g(x)的表达式,即可求解其最小值;
(2)通过集合A={x|[1+f(x)]•|f(x)|≥2},求出集合A,对于任意的x∈A,不等式2f-1(x+m)-g(x)≥0恒成立,转化为对数函数恒成立,进一步转化为二次函数恒成立问题,然后求实数m的取值范围.
(2)通过集合A={x|[1+f(x)]•|f(x)|≥2},求出集合A,对于任意的x∈A,不等式2f-1(x+m)-g(x)≥0恒成立,转化为对数函数恒成立,进一步转化为二次函数恒成立问题,然后求实数m的取值范围.
解答:
解:(1)函数f(x)=2x-1的反函数为y=f-1(x)=log2(x+1),x>-1
∴g(x)=f-1(x-1)=log2x.x>0.
∴函数y=2f-1(x)-g(x)=2log2(x+1)-log2x=log2
=log2
=log2(x+
+2),
∵x>0,∴x+
+2≥4,当且仅当x=1时取等号,
∴函数y=2f-1(x)-g(x)的最小值为:log24=2.
(2)∵集合A={x|[1+f(x)]•|f(x)|≥2},
∴[1+f(x)]•|f(x)|≥2,即2x|2x-1|≥2,
可得:
…①或
…②
解①得x≥1;解②得:x∈∅.
∴A={x|x≥1},
∴不等式2f-1(x+m)-g(x)≥0,化为2log2(x+m+1)-log2x≥0,
对于任意的x∈A,不等式2f-1(x+m)-g(x)≥0恒成立,
即对于任意的x∈A,不等式2log2(x+m+1)-log2x≥0恒成立,
∴表达式转化为:log2
≥0,在x≥1时恒成立;
即
≥1,在x≥1时恒成立;
(x+m+1)2≥x在x≥1时恒成立;
x2+(2m+1)x+(m+1)2≥0,在x≥1时恒成立;
令h(x)=x2+(2m+1)x+(m+1)2,函数的开口向上,要使在x≥1时恒成立;
必须满足
或△<0,
即
…①或(2m+1)2-4(m+1)2<0…②
解①得:m≥-1或m≤-3.
解②得:m>-
,
综上:m∈{m|m≥-1或m≤-3}.
∴g(x)=f-1(x-1)=log2x.x>0.
∴函数y=2f-1(x)-g(x)=2log2(x+1)-log2x=log2
| (x+1)2 |
| x |
| x2+2x+1 |
| x |
| 1 |
| x |
∵x>0,∴x+
| 1 |
| x |
∴函数y=2f-1(x)-g(x)的最小值为:log24=2.
(2)∵集合A={x|[1+f(x)]•|f(x)|≥2},
∴[1+f(x)]•|f(x)|≥2,即2x|2x-1|≥2,
可得:
|
|
解①得x≥1;解②得:x∈∅.
∴A={x|x≥1},
∴不等式2f-1(x+m)-g(x)≥0,化为2log2(x+m+1)-log2x≥0,
对于任意的x∈A,不等式2f-1(x+m)-g(x)≥0恒成立,
即对于任意的x∈A,不等式2log2(x+m+1)-log2x≥0恒成立,
∴表达式转化为:log2
| (x+m+1)2 |
| x |
即
| (x+m+1)2 |
| x |
(x+m+1)2≥x在x≥1时恒成立;
x2+(2m+1)x+(m+1)2≥0,在x≥1时恒成立;
令h(x)=x2+(2m+1)x+(m+1)2,函数的开口向上,要使在x≥1时恒成立;
必须满足
|
即
|
解①得:m≥-1或m≤-3.
解②得:m>-
| 3 |
| 4 |
综上:m∈{m|m≥-1或m≤-3}.
点评:本题考查函数恒成立问题,反函数以及对数函数基本不等式以及二次函数闭区间上的最值问题,考查转化思想以及分析问题解决问题的能力.

练习册系列答案
相关题目
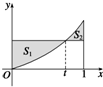 在区间[0,1]上给定曲线y=x2,试在此区间内确定点t的值,使图中阴影部分的面积:
在区间[0,1]上给定曲线y=x2,试在此区间内确定点t的值,使图中阴影部分的面积: