Question

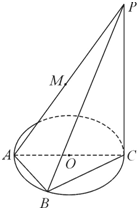如图，AC为圆O的直径，PC为圆O所在平面的垂线（C为垂足），B为半圆周上一点，M为AP的中点，且PC=4，AB=BC=2．
（1）求证：平面ABP⊥平面BPC；
（2）求三棱锥A-MBC的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,平面与平面垂直的判定

专题：综合题,空间位置关系与距离

分析：（1）证明AB⊥平面PBC，即可证明平面ABP⊥平面BPC；
（2）利用转换底面，V_A-MBC=V_M-ABC，即可求出三棱锥A-MBC的体积．

解答： （1）证明：∵PC⊥平面ABC，
∴PC⊥AB…（1分）
∵AC为圆O的直径，B为半圆周上一点
∴AB⊥BC…（2分）
又∵PC∩BC=C
∴AB⊥平面PBC，…（4分）
又AB?平面PAB
∴平面ABP⊥平面BPC…（6分）
（2）解：连结MO，则
∵PC⊥平面ABC
且M、O分别为AP、AC的中点，∴MO∥PC，且MO=

1

2

PC=2，
∴MO⊥平面ABC，…（8分）
∵AB⊥BC，∴S_△ABC=

1

2

×2×2=2，
∴V_A-MBC=V_M-ABC=

1

3

×2×2=

4

3

，…（12分）

点评：本题考查面面垂直，考查三棱锥A-MBC的体积，正确运用线面垂直的判定定理是关键．