题目内容
对于函数f(x)=a-
,x∈R
(1)若函数f(x)为奇函数,求实数a的值;
(2)探索函数f(x)的单调性;
(3)若f(logb(2t-t2))>f(logb(2-t))(b>0且b≠1),求实数t的取值范围.
| 2 |
| 2x+1 |
(1)若函数f(x)为奇函数,求实数a的值;
(2)探索函数f(x)的单调性;
(3)若f(logb(2t-t2))>f(logb(2-t))(b>0且b≠1),求实数t的取值范围.
考点:奇偶性与单调性的综合,函数单调性的判断与证明,函数奇偶性的性质
专题:函数的性质及应用
分析:(1)由函数f(x)为奇函数,f(0)=0,求得实数a的值.
(2)根据函数的解析式可得当x增大时,
变小,a-
变大,可得函数f(x)在R上是增函数.
(3)由f(logb(2t-t2))>f(logb(2-t))以及f(x)在R上是增函数可得单调性可得logb(2t-t2))>logb(2-t),分对数的底数大于1、和大于零小于1两种情况,分别求得t的范围.
(2)根据函数的解析式可得当x增大时,
| 2 |
| 2x+1 |
| 2 |
| 2x+1 |
(3)由f(logb(2t-t2))>f(logb(2-t))以及f(x)在R上是增函数可得单调性可得logb(2t-t2))>logb(2-t),分对数的底数大于1、和大于零小于1两种情况,分别求得t的范围.
解答:
解:(1)对于函数f(x)=a-
,x∈R,若函数f(x)为奇函数,则有f(0)=a-1=0,由此求得实数a=1.
(2)由于当x增大时,
变小,故a-
变大,故函数f(x)在R上是增函数.
(3)若f(logb(2t-t2))>f(logb(2-t)),则由f(x)在R上是增函数可得单调性可得logb(2t-t2))>logb(2-t),
当b>1时,2t-t2 >2-t,求得1<t<2,故实数t的取值范围为(1,2),
当0<b<1时,0<2t-t2 <2-t,求得1<t<2,故实数t的取值范围为(0,1).
| 2 |
| 2x+1 |
(2)由于当x增大时,
| 2 |
| 2x+1 |
| 2 |
| 2x+1 |
(3)若f(logb(2t-t2))>f(logb(2-t)),则由f(x)在R上是增函数可得单调性可得logb(2t-t2))>logb(2-t),
当b>1时,2t-t2 >2-t,求得1<t<2,故实数t的取值范围为(1,2),
当0<b<1时,0<2t-t2 <2-t,求得1<t<2,故实数t的取值范围为(0,1).
点评:本题主要考查函数的奇偶性和单调性的应用,属于基础题.

练习册系列答案
相关题目
 如图所示,四棱锥P-ABCD中,侧面PAD是正三角形,且与底面垂直,底面ABCD是菱形,∠BAD=60°,E为PC的中点.
如图所示,四棱锥P-ABCD中,侧面PAD是正三角形,且与底面垂直,底面ABCD是菱形,∠BAD=60°,E为PC的中点. 商丘是商部族的起源和聚居地,商人、商业的发源地和商朝最早的建都地.华商始祖王亥最早在这里,商丘是华商之都,于2006年11月10日在商丘举办首届国际华商文化节,某花卉集团根据需要欲将如图所示一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知AB=3米,AD=2米.
商丘是商部族的起源和聚居地,商人、商业的发源地和商朝最早的建都地.华商始祖王亥最早在这里,商丘是华商之都,于2006年11月10日在商丘举办首届国际华商文化节,某花卉集团根据需要欲将如图所示一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知AB=3米,AD=2米.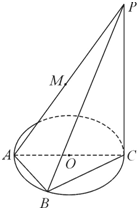 如图,AC为圆O的直径,PC为圆O所在平面的垂线(C为垂足),B为半圆周上一点,M为AP的中点,且PC=4,AB=BC=2.
如图,AC为圆O的直径,PC为圆O所在平面的垂线(C为垂足),B为半圆周上一点,M为AP的中点,且PC=4,AB=BC=2.