题目内容
设f(x)=ax3+bx+c(a≠0)为奇函数,其图象在点(1,f(1))处的切线为6x+y+4=0.
(1)求a,b,c的值;
(2)求f(x)的单调区间和极值.
(1)求a,b,c的值;
(2)求f(x)的单调区间和极值.
考点:利用导数研究函数的极值,利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)由f(x)为奇函数,得c=0.求导得f′(x)=3ax2+b,由已知得
,从而得到a=2,b=-12,c=0.
(2)由(1)得f(x)=2x3-12x.f′(x)=6x2-12=6(x+
)(x-
),列表讨论,能求出f(x)的单调区间和极值.
|
(2)由(1)得f(x)=2x3-12x.f′(x)=6x2-12=6(x+
| 2 |
| 2 |
解答:
解:(1)∵f(x)为奇函数,∴f(-x)=-f(x),
即-ax3-bx+c=-ax3-bx-c,∴c=0.
∵f(x)在点(1,f(1))处的切线为6x+y+4=0,
∴f(1)=y=-10,
求导得f′(x)=3ax2+b,∴
,
解得a=2,b=-12,
∴a=2,b=-12,c=0.…(6分)
(2)由(1)得f(x)=2x3-12x.∴f′(x)=6x2-12=6(x+
)(x-
),列表如下:
∴函数f(x)的单调增区间是(-∞,-
)和(
,+∞),单调减区间是(-
,
).
∴f(x)极大值=f(-
)=8
,f(x)极小值=-8
.…(12分)
即-ax3-bx+c=-ax3-bx-c,∴c=0.
∵f(x)在点(1,f(1))处的切线为6x+y+4=0,
∴f(1)=y=-10,
求导得f′(x)=3ax2+b,∴
|
解得a=2,b=-12,
∴a=2,b=-12,c=0.…(6分)
(2)由(1)得f(x)=2x3-12x.∴f′(x)=6x2-12=6(x+
| 2 |
| 2 |
| x | (-∞,-
| -
| (-
|
| (
| ||||||||||||
| f′(x) | + | 0 | - | 0 | + | ||||||||||||
| f(x) | ↑ | 极大值 | ↓ | 极小 | ↑ |
| 2 |
| 2 |
| 2 |
| 2 |
∴f(x)极大值=f(-
| 2 |
| 2 |
| 2 |
点评:本题主要考查极值的概念、利用导数研究函数的单调性等基础知识,同时考查推理论证能力,分类讨论等综合解题能力.解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,四棱锥P-ABCD中,侧面PAD是正三角形,且与底面垂直,底面ABCD是菱形,∠BAD=60°,E为PC的中点.
如图所示,四棱锥P-ABCD中,侧面PAD是正三角形,且与底面垂直,底面ABCD是菱形,∠BAD=60°,E为PC的中点.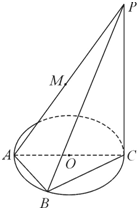 如图,AC为圆O的直径,PC为圆O所在平面的垂线(C为垂足),B为半圆周上一点,M为AP的中点,且PC=4,AB=BC=2.
如图,AC为圆O的直径,PC为圆O所在平面的垂线(C为垂足),B为半圆周上一点,M为AP的中点,且PC=4,AB=BC=2.