题目内容
已知函数f（x）=
x3+ax+b（a，b∈R）在x=2处取得的极小值是-
．
（Ⅰ）求a，b的值；
（Ⅱ）当x∈[-4，3]时，求函数f（x）的最大值与最小值．
| 1 |
| 3 |
| 4 |
| 3 |
（Ⅰ）求a，b的值；
（Ⅱ）当x∈[-4，3]时，求函数f（x）的最大值与最小值．
考点：利用导数研究函数的极值,利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题：计算题,导数的概念及应用
分析：（Ⅰ）求导函数，建立方程，可求a、b的值，从而可求a+b的值
（Ⅱ）比较端点值和极值得出函数f（x）的最大值与最小值．
（Ⅱ）比较端点值和极值得出函数f（x）的最大值与最小值．
解答：
解：（Ⅰ）求导函数，可得f′（x）=x2+a，
∵在x=2处取得的极小值是-
．
∴f′（2）=0，f（2）=-
．
4+a=0，
+2a+b=-
．
a=-4，b=4．
（Ⅱ）由（Ⅰ）知f′（x）=x2-4，由f′（x）=0，得x=2或-2．
比较端点值和极值得出函数f（x）的最大值与最小值：
f（-4）=-
，f（-2）=
，f（2）=-
，f（3）=1．
所以f（x）的最大值为
，最小值为-
．
∵在x=2处取得的极小值是-
| 4 |
| 3 |
∴f′（2）=0，f（2）=-
| 4 |
| 3 |
4+a=0，
| 8 |
| 3 |
| 4 |
| 3 |
a=-4，b=4．
（Ⅱ）由（Ⅰ）知f′（x）=x2-4，由f′（x）=0，得x=2或-2．
比较端点值和极值得出函数f（x）的最大值与最小值：
f（-4）=-
| 4 |
| 3 |
| 28 |
| 3 |
| 4 |
| 3 |
所以f（x）的最大值为
| 28 |
| 3 |
| 4 |
| 3 |
点评：本题考查导数知识的运用，考查函数的极值与最值，解题的关键是正确求导，理解极值与最值的含义．
练习册系列答案
相关题目
如图所示，四棱锥P-ABCD中，侧面PAD是正三角形，且与底面垂直，底面ABCD是菱形，∠BAD=60°，E为PC的中点．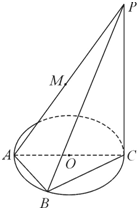
如图，AC为圆O的直径，PC为圆O所在平面的垂线（C为垂足），B为半圆周上一点，M为AP的中点，且PC=4，AB=BC=2．