题目内容
 如图,抛物线C:y=-
如图,抛物线C:y=-| 1 |
| 3 |
(1)求以F1,F2为焦点且过点P的椭圆方程;
(2)经过坐标原点O的直线l与抛物线相交于A,B两点,若|AO|=3|OB|,求直线l的方程.
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)求出P,F1,F2的坐标,可得a,b,c,即可求以F1,F2为焦点且过点P的椭圆方程;
(2)设l:y=kx,代入椭圆的方程,利用韦达定理及|AO|=3|OB|,即可求直线l的方程.
(2)设l:y=kx,代入椭圆的方程,利用韦达定理及|AO|=3|OB|,即可求直线l的方程.
解答:
解:(1)由y=-
x2+1解得P(0,1)、F1(-
,0)、F2(
,0),
所以b=1,c=
,从而a=2,
椭圆的方程为
+y2=1.----(5分)
(2)依题意设l:y=kx,代入椭圆的方程得x2+3kx-3=0.----(8分)
设A、B的坐标分别为A(x1,y1),B(x2,y2).
依题意得△>0,x1+x2=-3k,x1x2=-3,x1=-3x2,解得k=±
.----(10分)
所以,直线l的方程是y=
x或y=-
x.----(12分)
| 1 |
| 3 |
| 3 |
| 3 |
所以b=1,c=
| 3 |
椭圆的方程为
| x2 |
| 4 |
(2)依题意设l:y=kx,代入椭圆的方程得x2+3kx-3=0.----(8分)
设A、B的坐标分别为A(x1,y1),B(x2,y2).
依题意得△>0,x1+x2=-3k,x1x2=-3,x1=-3x2,解得k=±
| 2 |
| 3 |
所以,直线l的方程是y=
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题考查椭圆方程,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 商丘是商部族的起源和聚居地,商人、商业的发源地和商朝最早的建都地.华商始祖王亥最早在这里,商丘是华商之都,于2006年11月10日在商丘举办首届国际华商文化节,某花卉集团根据需要欲将如图所示一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知AB=3米,AD=2米.
商丘是商部族的起源和聚居地,商人、商业的发源地和商朝最早的建都地.华商始祖王亥最早在这里,商丘是华商之都,于2006年11月10日在商丘举办首届国际华商文化节,某花卉集团根据需要欲将如图所示一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知AB=3米,AD=2米.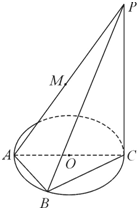 如图,AC为圆O的直径,PC为圆O所在平面的垂线(C为垂足),B为半圆周上一点,M为AP的中点,且PC=4,AB=BC=2.
如图,AC为圆O的直径,PC为圆O所在平面的垂线(C为垂足),B为半圆周上一点,M为AP的中点,且PC=4,AB=BC=2. 如图,在直三棱柱(侧棱垂直于底面)ABC-A1B1C1中,∠ACB=90°,CB=1,CA=
如图,在直三棱柱(侧棱垂直于底面)ABC-A1B1C1中,∠ACB=90°,CB=1,CA=