题目内容
已知函数f(x)=x3-3ax2+2bx在x=1处有极小值-1,试求a,b的值,并求出f(x)的极大值.
考点:利用导数研究函数的极值
专题:计算题,导数的概念及应用
分析:根据函数f(x)=x3-3ax2+2bx在x=1处有极小值-1,先求出函数中的参数a,b的值,再令导数等于0,求出极值点,判断极值点左右两侧导数的正负,当左正右负时有极大值,当左负右正时有极小值.再代入原函数求出极大值.
解答:
解:由已知,可得f(1)=1-3a+2b=-1①,
又f'(x)=3x2-6ax+2b,
∴f'(1)=3-6a+2b=0,②
由①,②,解得a=
,b=-
.
故函数的解析式为f(x)=x3-x2-x.
由此得f'(x)=3x2-2x-1,根据二次函数的性质,当x<-
或x>1时,f'(x)>0;
当-
<x<1,f'(x)<0.
∴函数f(x) 在(-∞,-
)和(1,+∞)上单调递增,在(-
,1)单调递减
∴当x=-
时,f(x)取得极大值,f(x)极大值=
又f'(x)=3x2-6ax+2b,
∴f'(1)=3-6a+2b=0,②
由①,②,解得a=
| 1 |
| 3 |
| 1 |
| 2 |
故函数的解析式为f(x)=x3-x2-x.
由此得f'(x)=3x2-2x-1,根据二次函数的性质,当x<-
| 1 |
| 3 |
当-
| 1 |
| 3 |
∴函数f(x) 在(-∞,-
| 1 |
| 3 |
| 1 |
| 3 |
∴当x=-
| 1 |
| 3 |
| 5 |
| 27 |
点评:本题主要考查函数的导数与极值之间的关系,属于导数的应用,比较基础.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
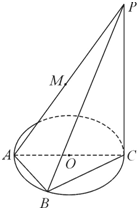 如图,AC为圆O的直径,PC为圆O所在平面的垂线(C为垂足),B为半圆周上一点,M为AP的中点,且PC=4,AB=BC=2.
如图,AC为圆O的直径,PC为圆O所在平面的垂线(C为垂足),B为半圆周上一点,M为AP的中点,且PC=4,AB=BC=2.