题目内容
某校从高一年级期末考试的学生中抽出20名学生,其成绩(均为整数)的频率分布直方图如图所示:

(1)估计这次考试中学生成绩在70到90分的概率;
(2)根据频率分布直方图估计平均分;
(3)从成绩是80分以上的学生中选两人,求他们在同一分数段的概率.

(1)估计这次考试中学生成绩在70到90分的概率;
(2)根据频率分布直方图估计平均分;
(3)从成绩是80分以上的学生中选两人,求他们在同一分数段的概率.
考点:等可能事件的概率
专题:应用题,概率与统计
分析:(1)根据频率分布直方图,可得这次考试中学生成绩在70到90分的概率;
(2)根据频率分布直方图,利用组中值估计平均分;
(3)确定基本事件的个数,即可求出在同一分数段的概率.
(2)根据频率分布直方图,利用组中值估计平均分;
(3)确定基本事件的个数,即可求出在同一分数段的概率.
解答:
 解:(1)70到90分的概率:0.03×10+0.025×10
解:(1)70到90分的概率:0.03×10+0.025×10
=0.3+0.25=0.55…(3分)
(2)平均分:45×0.05+55×0.15+65×0.2+75×0.30+85×0.25+95×0.05=72…(3分)
(3)80到90分人数:0.025×10×20=5(人)
90到100分人数:0.005×10×20=1(人)…(2分)
设90到100分的人为a,80到90分的5个人分别为:1、2、3、4、5,则有(a,1)、(a,2)、(a,3)、(a,4)、(a,5)、(1,2)、(1,3)、(1,4)、(1,5)、(2,3)、(2,4)、(2,5)、(3,4)、(3,5)、(4,5)15个基本事件,且他们是等可能的,…(3分)
设事件A为选中的两人在同一分数段,则事件A有(1,2)、(1,3)、(1,4)、(1,5)、(2,3)、(2,4)、(2,5)、(3,4)、(3,5)、(4,5)10个基本事件,…(2分)
∴P(A)=
=
…(1分)
答:(1)70到9(0分)的概率为0.55;
(2)平均分为72;
(3)成绩是8(0分)以上(包括80分)的学生中选中的两人在同一分数段的概率为
.
 解:(1)70到90分的概率:0.03×10+0.025×10
解:(1)70到90分的概率:0.03×10+0.025×10=0.3+0.25=0.55…(3分)
(2)平均分:45×0.05+55×0.15+65×0.2+75×0.30+85×0.25+95×0.05=72…(3分)
(3)80到90分人数:0.025×10×20=5(人)
90到100分人数:0.005×10×20=1(人)…(2分)
设90到100分的人为a,80到90分的5个人分别为:1、2、3、4、5,则有(a,1)、(a,2)、(a,3)、(a,4)、(a,5)、(1,2)、(1,3)、(1,4)、(1,5)、(2,3)、(2,4)、(2,5)、(3,4)、(3,5)、(4,5)15个基本事件,且他们是等可能的,…(3分)
设事件A为选中的两人在同一分数段,则事件A有(1,2)、(1,3)、(1,4)、(1,5)、(2,3)、(2,4)、(2,5)、(3,4)、(3,5)、(4,5)10个基本事件,…(2分)
∴P(A)=
| 10 |
| 15 |
| 2 |
| 3 |
答:(1)70到9(0分)的概率为0.55;
(2)平均分为72;
(3)成绩是8(0分)以上(包括80分)的学生中选中的两人在同一分数段的概率为
| 2 |
| 3 |
点评:本题考主要查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,列举法,是解决古典概型问题的一种重要的解题方法,属于基础题.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
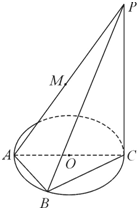 如图,AC为圆O的直径,PC为圆O所在平面的垂线(C为垂足),B为半圆周上一点,M为AP的中点,且PC=4,AB=BC=2.
如图,AC为圆O的直径,PC为圆O所在平面的垂线(C为垂足),B为半圆周上一点,M为AP的中点,且PC=4,AB=BC=2. 如图,在直三棱柱(侧棱垂直于底面)ABC-A1B1C1中,∠ACB=90°,CB=1,CA=
如图,在直三棱柱(侧棱垂直于底面)ABC-A1B1C1中,∠ACB=90°,CB=1,CA=