题目内容
已知在函数f(x)=mx3-x的图象上以N(1,n)为切点的切线的倾斜角为
.
(Ⅰ)求m、n的值;
(Ⅱ)是否存在最小的正整数k,使得不等式f(x)≤k-2013对于x∈[-1,3]恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
(Ⅲ)求证:|f(sinx)+f(cosx)|≤2f(t+
),(x∈R,t>0).
| π |
| 4 |
(Ⅰ)求m、n的值;
(Ⅱ)是否存在最小的正整数k,使得不等式f(x)≤k-2013对于x∈[-1,3]恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
(Ⅲ)求证:|f(sinx)+f(cosx)|≤2f(t+
| 1 |
| 2t |
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:函数的性质及应用,导数的综合应用
分析:(Ⅰ)利用导数的几何意义得tan
=f′(1),即1=3m-1,m=
,再将(1,n)代入f(x)=mx3-x求得n
(Ⅱ)不等式f(x)≤k-2013对于x∈[-1,3]恒成立,只需f(x)min≤k-2013,转化为求f(x)min
(Ⅲ)方法一:利用三角函数公式得出|f(sinx)+f(cosx)|=|(
sin3x-sinx)+(
cos3x-cosx)|=
|
sin(x+
)|3≤
.利用f(x)在(
,+∞)为增函数,得出2f(t+
)≥2f(
)=
,不等式可证.
方法二:由(Ⅱ)得出的单调性,可以证出x∈[-1,1]时,-
≤f(x)≤
,即f(x)|≤
,
由于sinx,cosx∈[-1,1]所以|f(sinx)|≤
,|f(cos)|≤
,|f(sinx)+f(cosx)|≤
,利用f(x)在(
,+∞)为增函数,得出2f(t+
)≥2f(
)=
,不等式可证.
| π |
| 4 |
| 2 |
| 3 |
(Ⅱ)不等式f(x)≤k-2013对于x∈[-1,3]恒成立,只需f(x)min≤k-2013,转化为求f(x)min
(Ⅲ)方法一:利用三角函数公式得出|f(sinx)+f(cosx)|=|(
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| π |
| 4 |
2
| ||
| 3 |
| ||
| 2 |
| 1 |
| 2t |
| ||
| 2 |
2
| ||
| 3 |
方法二:由(Ⅱ)得出的单调性,可以证出x∈[-1,1]时,-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
由于sinx,cosx∈[-1,1]所以|f(sinx)|≤
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
| ||
| 2 |
| 1 |
| 2t |
| ||
| 2 |
2
| ||
| 3 |
解答:
解:(Ⅰ)f′(x)=3mx2-1,依题意,得tan
=f′(1),即1=3m-1,m=
∴f(x)=
x3-x,把N(1,n)代得,得n=f(1)=-
,
∴m=
,n=-
(Ⅱ)令f′(x)=2(x+
)(x-
)=0,则x=±
,
当-1<x<-
时,f′(x)=2x2-1>0,f(x)在此区间为增函数
当-
<x<
时,f′(x)=2x2-1<0,f(x)在此区间为减函数
当
<x<3时,f′(x)=2x2-1>0,),f(x)在此区间为增函数
又f(-
)=
,f(3)=15,
因此,当x∈[-1,3]时,-
≤f(x)≤15,
要使得不等式f(x)≤k-2013对于x∈[-1,3]恒成立,则k≥15+2013=2028
所以,存在最小的正整数k=2028,
使得不等式f(x)≤k-2013对于x∈[-1,3]恒成立.
(Ⅲ)(方法一)|f(sinx)+f(cosx)|=|(
sin3x-sinx)+(
cos3x-cosx)|=|
(sin3+cos3x)-(sinx+cosx)|=|(sinx+cosx)[
(sin2x-sinxcosx+cos2x)-1]|=|sinx+cosx|•|
sinxcosx+
|=
|sinx+cosx|3=
|
sin(x+
)|3≤
.
又∵t>0∴t+
≥
,由(2)知f(x)在(
,+∞)为增函数,∴2f(t+
)≥2f(
)=
综上可得:|f(sinx)+f(cosx)|≤2f(t+
)(x∈R,t>0).
(方法二)由(Ⅱ)知,函数f(x)在[-1,-
]上是增函数;在[-
,
]
上是减函数,在[
,1]上是增函数
又f(-1)=
,f(-
)=
,f(
)=-
,f(1)=-
所以,当x∈[-1,1]时,-
≤f(x)≤
,即f(x)|≤
,
∵sinx,cosx∈[-1,1]∴|f(sinx)|≤
,|f(cos)|≤
.
∴|f(sinx)+f(cosx)|≤|f(sinx)|+|f(cosx)|≤
+
=
又t>0,∴t+
≥
>1,且函数f(x)在[1,+∞]上是增函数,
∴2f(t+
)≥2f(
)=2[
(
)3-
]=
综上可得:|f(sinx)+f(cosx)|≤2f(t+
)(x∈R,t>0)
| π |
| 4 |
| 2 |
| 3 |
∴f(x)=
| 2 |
| 3 |
| 1 |
| 3 |
∴m=
| 2 |
| 3 |
| 1 |
| 3 |
(Ⅱ)令f′(x)=2(x+
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
当-1<x<-
| ||
| 2 |
当-
| ||
| 2 |
| ||
| 2 |
当
| ||
| 2 |
又f(-
| ||
| 2 |
2
| ||
| 3 |
因此,当x∈[-1,3]时,-
| ||
| 3 |
要使得不等式f(x)≤k-2013对于x∈[-1,3]恒成立,则k≥15+2013=2028
所以,存在最小的正整数k=2028,
使得不等式f(x)≤k-2013对于x∈[-1,3]恒成立.
(Ⅲ)(方法一)|f(sinx)+f(cosx)|=|(
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| π |
| 4 |
2
| ||
| 3 |
又∵t>0∴t+
| 1 |
| 2t |
| 2 |
| ||
| 2 |
| 1 |
| 2t |
| 2 |
2
| ||
| 3 |
综上可得:|f(sinx)+f(cosx)|≤2f(t+
| 1 |
| 2t |
(方法二)由(Ⅱ)知,函数f(x)在[-1,-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
上是减函数,在[
| ||
| 2 |
又f(-1)=
| 1 |
| 3 |
| ||
| 2 |
| ||
| 3 |
| ||
| 2 |
| ||
| 3 |
| 1 |
| 3 |
所以,当x∈[-1,1]时,-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
∵sinx,cosx∈[-1,1]∴|f(sinx)|≤
| ||
| 3 |
| ||
| 3 |
∴|f(sinx)+f(cosx)|≤|f(sinx)|+|f(cosx)|≤
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
又t>0,∴t+
| 1 |
| 2t |
| 2 |
∴2f(t+
| 1 |
| 2t |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
2
| ||
| 3 |
综上可得:|f(sinx)+f(cosx)|≤2f(t+
| 1 |
| 2t |
点评:本题考查函数的单调性与导数,函数性质的应用,不等式的证明与不等式恒成立,考查分析解决问题能力,研究出函数的性质,再应用性质解决问题需要较高的数学能力.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
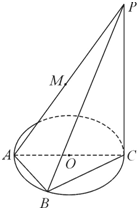 如图,AC为圆O的直径,PC为圆O所在平面的垂线(C为垂足),B为半圆周上一点,M为AP的中点,且PC=4,AB=BC=2.
如图,AC为圆O的直径,PC为圆O所在平面的垂线(C为垂足),B为半圆周上一点,M为AP的中点,且PC=4,AB=BC=2.