题目内容
13.已知双曲线C的焦点、实轴端点恰好分别是椭圆$\frac{x^2}{16}+\frac{y^2}{7}=1$的长轴端点、焦点,则双曲线C的渐近线方程是$y=±\frac{{\sqrt{7}}}{3}x$.分析 利用椭圆的性质可得其长轴的端点、焦点,进而得到双曲线的c,a,b,即可得到双曲线的渐近线方程.
解答 解:椭圆长轴端点为(-4,0),(4,0),焦点为(-3,0),(3,0),
∴对于双曲线中,c=4,a=3,得b=$\sqrt{7}$,
∴双曲线的渐近线方程为:$y=±\frac{{\sqrt{7}}}{3}x$,
故答案为$y=±\frac{{\sqrt{7}}}{3}x$.
点评 熟练掌握椭圆与双曲线的标准方程及其性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.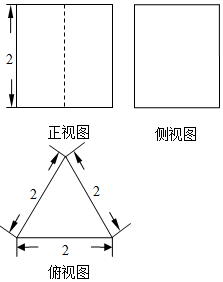 如图所示,是一个空间几何体的三视图,且这个空间几何体的所有顶点都在同一个球面上,则这个球的体积是( )
如图所示,是一个空间几何体的三视图,且这个空间几何体的所有顶点都在同一个球面上,则这个球的体积是( )
 如图所示,是一个空间几何体的三视图,且这个空间几何体的所有顶点都在同一个球面上,则这个球的体积是( )
如图所示,是一个空间几何体的三视图,且这个空间几何体的所有顶点都在同一个球面上,则这个球的体积是( )| A. | $\frac{49}{9}π$ | B. | $\frac{{28\sqrt{21}}}{27}π$ | C. | $\frac{28}{3}π$ | D. | $\frac{{28\sqrt{7}}}{9}π$ |
8.下列说法错误的是( )
| A. | 在△ABC中,若A>B,则cosA<cosB | |
| B. | 若b2=ac,则a,c的等比中项为b | |
| C. | 若命题p与p∧q为真,则q一定为真 | |
| D. | 若p:?x∈(0,+∞),lnx<x-1,则¬p:?x∈(0,+∞),lnx≥x-1 |
18.函数$y=tan(2x-\frac{π}{3})$的最小正周期是( )
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
9.已知$\overrightarrow a=({1,2,3}),\overrightarrow b=({-1,1,x})$,且$\overrightarrow a⊥\overrightarrow b$,则x的值为( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
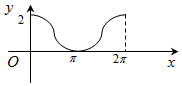
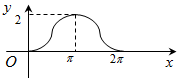
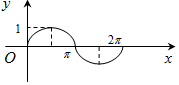
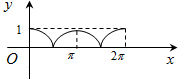
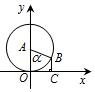 如图,圆A的半径为1,且A点的坐标为(0,1),B为圆上的动点,角α的始边为射线AO,终边为射线AB,过点B作x轴的垂线,垂足为C,将BC表示成α的函数f(α),则y=f(α)在[0,2π]的在图象大致为( )
如图,圆A的半径为1,且A点的坐标为(0,1),B为圆上的动点,角α的始边为射线AO,终边为射线AB,过点B作x轴的垂线,垂足为C,将BC表示成α的函数f(α),则y=f(α)在[0,2π]的在图象大致为( )