题目内容
9.已知$\overrightarrow a=({1,2,3}),\overrightarrow b=({-1,1,x})$,且$\overrightarrow a⊥\overrightarrow b$,则x的值为( )| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
分析 $\overrightarrow a⊥\overrightarrow b$,可得$\overrightarrow{a}•\overrightarrow{b}$=0,解得x.
解答 解:∵$\overrightarrow a⊥\overrightarrow b$,∴$\overrightarrow{a}•\overrightarrow{b}$=-1+2+3x=0,解得x=-$\frac{1}{3}$.
故选:B.
点评 本题考查了向量垂直与数量积的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
14.若函数y=ax+m-1 (a>0,a≠1)的图象在第一、三、四象限内,则( )
| A. | a>1 | B. | a>1,且m<0 | C. | 0<a<1,且m>0 | D. | 0<a<1 |
14.已知函数$f(x)=\left\{\begin{array}{l}({3-a})x-1,x≤5\\{a^{x-4}},x>5\end{array}\right.({a>0,a≠1})$,数列{an}满足${a_n}=f(n)({n∈{N^*}})$,且{an}是单调递增数列,则实数a的取值范围是( )
| A. | (1,3) | B. | (2,3) | C. | $[{\frac{7}{3},3})$ | D. | $({1,\frac{7}{3}}]$ |
19.关于x的方程4x-m•2x+1+4=0有实数根,则m的取值范围( )
| A. | (1,+∞) | B. | [1,+∞) | C. | (2,+∞) | D. | [2,+∞) |
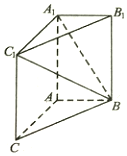 如图,在三棱柱ABC-A1B1C1中,平面ABC⊥平面AA1B1B,四边形AA1B1B是矩形,且AB=1,AC=2,BC=$\sqrt{5}$.
如图,在三棱柱ABC-A1B1C1中,平面ABC⊥平面AA1B1B,四边形AA1B1B是矩形,且AB=1,AC=2,BC=$\sqrt{5}$.