题目内容
已知a>0且a≠1,f(x)=x2,g(x)=ax+
,当x∈(-1,1)时f(x)<g(x)恒成立,则实数a的取值范围 .
| 1 |
| 4 |
考点:指数函数单调性的应用
专题:函数的性质及应用
分析:转化为ax≥
,x∈(-1,1)上恒成立,再分类讨论最小值恒大于或等于
,求解即可.
| 3 |
| 4 |
| 3 |
| 4 |
解答:
解:∵f(x)=x2,x∈(-1,1),
∴f(x)∈[0,1)
∵f(x)<g(x)恒成立
∴只需g(x)≥1即可.
∵g(x)=ax+
≥1,
∴ax≥
,x∈(-1,1)上恒成立,
当a>1时,a-1≥
,即1<a≤
,
当0<a<1时,a1≥
,即
≤a<1,
故实数a的取值范围为:[
,1)∪(1,
]
∴f(x)∈[0,1)
∵f(x)<g(x)恒成立
∴只需g(x)≥1即可.
∵g(x)=ax+
| 1 |
| 4 |
∴ax≥
| 3 |
| 4 |
当a>1时,a-1≥
| 3 |
| 4 |
| 4 |
| 3 |
当0<a<1时,a1≥
| 3 |
| 4 |
| 3 |
| 4 |
故实数a的取值范围为:[
| 3 |
| 4 |
| 4 |
| 3 |
点评:本题考察了指数函数的单调性,不等式的恒成立问题,属于中档题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
函数y=x2-x,(-1<x<4)值域是( )
A、[-
| ||
| B、(2,12) | ||
| C、( 2,20) | ||
D、[-
|
如果在约束条件
(0<a<1)下,目标函数x+ay最大值是
,则a=( )
|
| 5 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图,当x1=6,x2=9,p=8.5时,x3等于( )
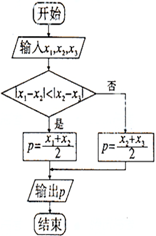

| A、8 | B、4 | C、10 | D、9 |