题目内容
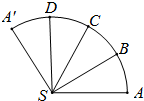如图是圆锥SO（O为底面中心）的侧面展开图，B，C，D是其侧面展开图中弧 |
| AA′ |
| A、∠SAB是直线SA与CD所成的角 |
| B、∠SAC是直线SA与平面ABCD所成的角 |
| C、平面SAC⊥平面SBD |
| D、∠SAD是二面角S-AB-D的平面角 |
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：画出圆锥的直观图与侧面展开图，
根据异面直线所成角的定义判定A正确；利用圆锥的性质证明线面垂直，根据线面角的定义判定B正确；
利用面面垂直的判定定理证明平面SAC⊥平面SBD，可得C正确；根据二面角的平面角的性质，判断D错误．
根据异面直线所成角的定义判定A正确；利用圆锥的性质证明线面垂直，根据线面角的定义判定B正确；
利用面面垂直的判定定理证明平面SAC⊥平面SBD，可得C正确；根据二面角的平面角的性质，判断D错误．
解答：
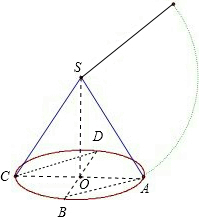
解：如图连接CD，AB，∵B，C，D是其侧面展开图的四等分点，∴AB∥CD，
∴∠SAB是直线SA与CD所成的角，故A正确；
∵AC为底面圆的直径，∴SO⊥底面ABCD，∴AC为SA在底面ABCD中的射影，
∴∠SAC为直线SA与平面ABCD所成的角，故B正确；
∵BD⊥AC，BD⊥SO，SO∩AC=O，∴BD⊥平面SAC，又BD?平面SBD，∴平面SAC⊥平面SBD，故C正确；
∵SA与AB不垂直，∴∠SAD不是二面角S-AB-D的平面角，故D错误．
故选D．
∴∠SAB是直线SA与CD所成的角，故A正确；
∵AC为底面圆的直径，∴SO⊥底面ABCD，∴AC为SA在底面ABCD中的射影，
∴∠SAC为直线SA与平面ABCD所成的角，故B正确；
∵BD⊥AC，BD⊥SO，SO∩AC=O，∴BD⊥平面SAC，又BD?平面SBD，∴平面SAC⊥平面SBD，故C正确；
∵SA与AB不垂直，∴∠SAD不是二面角S-AB-D的平面角，故D错误．
故选D．
点评：本题考查了圆锥的侧面展开图，异面直线所成的角的定义、线面角的定义及二面角的平面角的定义，涉及知识面广，对培养学生的空间想象能力及推理论证能力有很好的体现．
练习册系列答案
相关题目
函数f（x）=x3-3x+2在x∈[0，2]的最小值为（ ）
| A、-1 | B、0 | C、2 | D、4 |
已知直线l1：3x+2ay-5=0，l2：（3a-1）x-ay-2=0，若l1∥l2，则a的值为（ ）
A、-
| ||
| B、6 | ||
| C、0 | ||
D、0或-
|