题目内容
设数列
,
,
,
,
,
,…
,
…
…这个数列第2010项的值是 ;这个数列中,第2010个值为1的项的序号是 .
| 1 |
| 1 |
| 1 |
| 2 |
| 2 |
| 1 |
| 1 |
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
| 1 |
| k |
| 2 |
| k-1 |
| k |
| 1 |
考点:数列的概念及简单表示法
专题:等差数列与等比数列
分析:(1)将数列分组:(
),(
,
),(
,
,
),…,(
,
,…,
),…由此能求出数列的第2010项的值.
(2)由以上分组可以知道,每个奇数组中出现一个1,第2010个1出现在第4019组,由此能求出第2010个值为1的项的序号.
| 1 |
| 1 |
| 1 |
| 2 |
| 2 |
| 1 |
| 1 |
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
| 1 |
| k |
| 2 |
| k-1 |
| k |
| 1 |
(2)由以上分组可以知道,每个奇数组中出现一个1,第2010个1出现在第4019组,由此能求出第2010个值为1的项的序号.
解答:
解:(1)将数列分组:(
),(
,
),(
,
,
),…,
(
,
,…,
),…
∵1+2+3+…+62=1953;
1+2+3+…+63=2016,
所以数列的第2010项属于第63组倒数第7个数,即为
.
(2)由以上分组可以知道,每个奇数组中出现一个1,
∴第2010个1出现在第4019组,
而第4019组中的1位于该组第2010位,
∴第2010个值为1的项的序号为:
(1+2+3+…+4018)+2010=809428.
故答案为:
,809428.
| 1 |
| 1 |
| 1 |
| 2 |
| 2 |
| 1 |
| 1 |
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
(
| 1 |
| k |
| 2 |
| k-1 |
| k |
| 1 |
∵1+2+3+…+62=1953;
1+2+3+…+63=2016,
所以数列的第2010项属于第63组倒数第7个数,即为
| 57 |
| 7 |
(2)由以上分组可以知道,每个奇数组中出现一个1,
∴第2010个1出现在第4019组,
而第4019组中的1位于该组第2010位,
∴第2010个值为1的项的序号为:
(1+2+3+…+4018)+2010=809428.
故答案为:
| 57 |
| 7 |
点评:本题考查数列中某项值的求法,是中档题,解题时要认真审题,注意观察、归纳、总结能力的培养.

练习册系列答案
相关题目
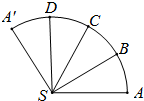 如图是圆锥SO(O为底面中心)的侧面展开图,B,C,D是其侧面展开图中弧
如图是圆锥SO(O为底面中心)的侧面展开图,B,C,D是其侧面展开图中弧 |
| AA′ |
| A、∠SAB是直线SA与CD所成的角 |
| B、∠SAC是直线SA与平面ABCD所成的角 |
| C、平面SAC⊥平面SBD |
| D、∠SAD是二面角S-AB-D的平面角 |