题目内容
函数f(x)=
,则下列说法中正确命题的个数是( )
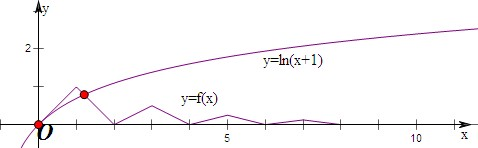
①函数y=f(x)-ln(x+1)有3个零点;
②若x>0时,函数f(x)≤
恒成立,则实数k的取值范围是[
,+∞);
③函数f(x)的极大值中一定存在最小值;
④f(x)=2kf(x+2k),(k∈N),对于一切x∈[0,+∞)恒成立.
|
①函数y=f(x)-ln(x+1)有3个零点;
②若x>0时,函数f(x)≤
| k |
| x |
| 3 |
| 2 |
③函数f(x)的极大值中一定存在最小值;
④f(x)=2kf(x+2k),(k∈N),对于一切x∈[0,+∞)恒成立.
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用,函数恒成立问题,根的存在性及根的个数判断
专题:数形结合
分析:①分别画出y=f(x)和y=ln(x+1)的图象,找其交点个数;②画出y=
的图象,通过k的变化,观察双曲线的变化,找出在y=f(x)图象上方的k值;③通过f(x)的图象得到;④不完全归纳得到f(x)的解析式.
| 1 |
| x |
解答:
解:①先画出y=1-|x-2|(0≤x≤2)的图象C,由f(x)=
f(x-2)(x>2)得:将C的图象向右平移2k(k∈N*)个单位,再将纵坐标缩小为
(k∈N*)倍,再画出y=ln(x+1)的图象,发现有2个交点,故①错;
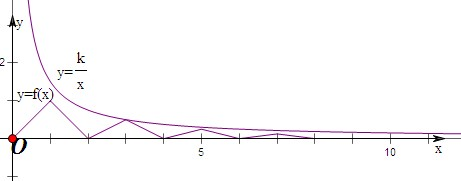
②画出y=
(x>0)的图象,观察k的变化,当图象过点(3,
)时,图象恒在y=f(x)的图象上,此时
k=
,所以实数k的取值范围是[
,+∞),故②正确;
③由y=f(x)的图象可知,f(x)的极大值中不存在最小值0,故③错;
④当k=0,0<X<2时,f(x)=20f(x)=1-|X-1|;当2<x<4时,f(x)=
f(x-2);
当4<x<6时,f(x)=
f(x-4),…,当2k<x<2k+2时,f(x)=
f(x-2k),
即有f(x-2k)=2kf(x),从而有f(x)=2kf(x+2k)),(k∈N),
对于一切x∈[0,+∞)恒成立,故④正确.
故选:B.
| 1 |
| 2 |
| 1 |
| 2k |

②画出y=
| k |
| x |
| 1 |
| 2 |
k=
| 3 |
| 2 |
| 3 |
| 2 |

③由y=f(x)的图象可知,f(x)的极大值中不存在最小值0,故③错;
④当k=0,0<X<2时,f(x)=20f(x)=1-|X-1|;当2<x<4时,f(x)=
| 1 |
| 2 |
当4<x<6时,f(x)=
| 1 |
| 4 |
| 1 |
| 2k |
即有f(x-2k)=2kf(x),从而有f(x)=2kf(x+2k)),(k∈N),
对于一切x∈[0,+∞)恒成立,故④正确.
故选:B.
点评:本题主要考查分段函数的图象和性质,以及函数的零点、恒成立问题,函数解析式求法,意在考查运用数形结合数学思想方法解决问题的能力,是一道中档题.

练习册系列答案
相关题目
已知三个集合E={x|x=m+
,m∈Z},F={x|x=
-
,n∈Z},G={x|x=
+
,p∈Z},则( )
| 1 |
| 6 |
| n |
| 2 |
| 1 |
| 3 |
| p |
| 2 |
| 1 |
| 6 |
| A、E=F?G |
| B、E?F=G |
| C、E⊆F?G |
| D、E?F?G |
若复数
是纯虚数(i是虚数单位),则实数a的值为( )
| -6+ai |
| 1+2i |
| A、6 | B、-6 | C、3 | D、-3 |
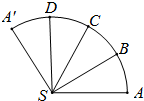 如图是圆锥SO(O为底面中心)的侧面展开图,B,C,D是其侧面展开图中弧
如图是圆锥SO(O为底面中心)的侧面展开图,B,C,D是其侧面展开图中弧 |
| AA′ |
| A、∠SAB是直线SA与CD所成的角 |
| B、∠SAC是直线SA与平面ABCD所成的角 |
| C、平面SAC⊥平面SBD |
| D、∠SAD是二面角S-AB-D的平面角 |