题目内容
有下列四种说法:
①命题:“?x0∈R,使得x2-x>0”的否定是“?x∈R,都有x2-x≤0”;
②已知随机变量x服从正态分布N(1,σ2),P(x≤4)=0.79,则P(x≤-2)=0.21;
③函数f(x)=2sinxcosx-1,(x∈R)图象关于直线x=
对称,且在区间[-
,
]上是增函数;
④设实数x,y∈[0,1],则满足:x2+y2<1的概率为
.
其中错误的个数是( )
①命题:“?x0∈R,使得x2-x>0”的否定是“?x∈R,都有x2-x≤0”;
②已知随机变量x服从正态分布N(1,σ2),P(x≤4)=0.79,则P(x≤-2)=0.21;
③函数f(x)=2sinxcosx-1,(x∈R)图象关于直线x=
| 3π |
| 4 |
| π |
| 4 |
| π |
| 4 |
④设实数x,y∈[0,1],则满足:x2+y2<1的概率为
| π |
| 4 |
其中错误的个数是( )
| A、0 | B、1 | C、2 | D、3 |
考点:正态分布曲线的特点及曲线所表示的意义,命题的真假判断与应用
专题:概率与统计,简易逻辑
分析:①由全称命题与存在性命题的否定推断;②运用正态分布的特点可计算求得;③运用正弦函数的对称轴方程和单调增区间判断;④由几何概率知识可得.
解答:
解:由含有一个量词的命题的否定得①显然正确;
由②可得μ=1(即平均数为1),P(x≥4)=1-0.79=0.21,
又图象对称轴为x=μ=1,所以P(x≤-2)=P(x≥4)=0.21,故②正确;
③由于函数f(x)=2sinxcosx-1,(x∈R),
即f(x)=sin(2x)-1的对称轴为x=
+
(k∈Z),
单调增区间为[kπ-
,kπ+
](k∈Z),所以f(x)的图象关于直线x=
对称,
且在区间[-
,
]上是增函数,故③正确;
④这是几何概率,区域D:边长为1的正方形,区域d:第一象限内的
个单位圆,
测度:面积,所以满足:x2+y2<1的概率是
,故④正确.
故选:A
由②可得μ=1(即平均数为1),P(x≥4)=1-0.79=0.21,
又图象对称轴为x=μ=1,所以P(x≤-2)=P(x≥4)=0.21,故②正确;
③由于函数f(x)=2sinxcosx-1,(x∈R),
即f(x)=sin(2x)-1的对称轴为x=
| kπ |
| 2 |
| π |
| 4 |
单调增区间为[kπ-
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
且在区间[-
| π |
| 4 |
| π |
| 4 |
④这是几何概率,区域D:边长为1的正方形,区域d:第一象限内的
| 1 |
| 4 |
测度:面积,所以满足:x2+y2<1的概率是
| π |
| 4 |
故选:A
点评:本题考查简易逻辑的基础知识:命题的否定,以及正弦函数的对称轴和单调区间,几何概率问题,意在考查学生的综合运用知识的能力,是一道基础题.

练习册系列答案
相关题目
若复数
是纯虚数(i是虚数单位),则实数a的值为( )
| -6+ai |
| 1+2i |
| A、6 | B、-6 | C、3 | D、-3 |
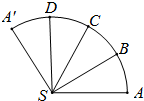 如图是圆锥SO(O为底面中心)的侧面展开图,B,C,D是其侧面展开图中弧
如图是圆锥SO(O为底面中心)的侧面展开图,B,C,D是其侧面展开图中弧 |
| AA′ |
| A、∠SAB是直线SA与CD所成的角 |
| B、∠SAC是直线SA与平面ABCD所成的角 |
| C、平面SAC⊥平面SBD |
| D、∠SAD是二面角S-AB-D的平面角 |
可导函数在闭区间的最大值必在( )
| A、取得极值点 |
| B、导数为0的点 |
| C、极值点或区间端点 |
| D、区间端点 |