题目内容
函数f（x）=x3-3x+2在x∈[0，2]的最小值为（ ）
| A、-1 | B、0 | C、2 | D、4 |
考点：利用导数求闭区间上函数的最值
专题：计算题,导数的概念及应用
分析：求出导数，由导数可得函数极值，进而可判断即为函数最值．
解答：
解：∵f（x）=x3-3x+2，
∴f'（x）=3x2-3=3（x+1）（x-1），
当0≤x＜1时，f'（x）＜0，f（x）单调递减；
当1＜x≤2时，f'（x）＞0，f（x）单调递增；
∴当x=1时f（x）取得极小值，也为最小值，f（1）=1-3+2=0，
∴f（x）在[0，2]上的最小值为0，
故选：B．
∴f'（x）=3x2-3=3（x+1）（x-1），
当0≤x＜1时，f'（x）＜0，f（x）单调递减；
当1＜x≤2时，f'（x）＞0，f（x）单调递增；
∴当x=1时f（x）取得极小值，也为最小值，f（1）=1-3+2=0，
∴f（x）在[0，2]上的最小值为0，
故选：B．
点评：本题考查利用导数求函数的最值问题，属中档题，连续函数在闭区间上的最值，要么在极值处取得，要么在区间端点处取得．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
已知三个集合E={x|x=m+
，m∈Z}，F={x|x=
-
，n∈Z}，G={x|x=
+
，p∈Z}，则（ ）
| 1 |
| 6 |
| n |
| 2 |
| 1 |
| 3 |
| p |
| 2 |
| 1 |
| 6 |
| A、E=F?G |
| B、E?F=G |
| C、E⊆F?G |
| D、E?F?G |
在（1-x）3（1+x）8的展开式中，含x2项的系数是n，若(8-nx)n=a0+a1x+a2x2+…+anxn，则a1+a2+…+an=（ ）
| A、1 |
| B、-1 |
| C、1-87 |
| D、-1+87 |
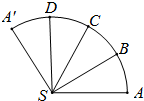如图是圆锥SO（O为底面中心）的侧面展开图，B，C，D是其侧面展开图中弧 |
| AA′ |
| A、∠SAB是直线SA与CD所成的角 |
| B、∠SAC是直线SA与平面ABCD所成的角 |
| C、平面SAC⊥平面SBD |
| D、∠SAD是二面角S-AB-D的平面角 |