题目内容
已知O是△ABC所在平面上一点，且
+2
+3
=
，则△OBC和△ABC的面积比为 ．
| OA |
| OB |
| OC |
| 0 |
考点：向量的加法及其几何意义
专题：平面向量及应用
分析：画出图形，结合图形，得出△OBC和△ABC面积比为|OM|：|AM|；根据题意，得出
与
的关系，从而求出两三角形的面积比．
| OM |
| OA |
解答：
解：如图，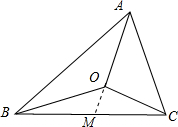
；
设直线AO与直线BC的交点为点M，则
△OBC和△ABC面积比为|OM|：|AM|；
设
=x
，
∵
+2
+3
=
，
∴
=x
=x（-2
-3
）=-2x
-3x
；
由平面向量的基本定理得，-2x-3x=1，
解得x=-
；
∴△OBC和△ABC的面积比为
|OM|：|AM|=
：（
+1）=1：6；
故答案为：1：6．
；设直线AO与直线BC的交点为点M，则
△OBC和△ABC面积比为|OM|：|AM|；
设
| OM |
| OA |
∵
| OA |
| OB |
| OC |
| 0 |
∴
| OM |
| OA |
| OB |
| OC |
| OB |
| OC |
由平面向量的基本定理得，-2x-3x=1，
解得x=-
| 1 |
| 5 |
∴△OBC和△ABC的面积比为
|OM|：|AM|=
| 1 |
| 5 |
| 1 |
| 5 |
故答案为：1：6．
点评：本题考查了平面向量的基本定理的应用问题，解题时应按照平面向量的运算法则进行解答，是基础题．
练习册系列答案
相关题目
已知三个集合E={x|x=m+
，m∈Z}，F={x|x=
-
，n∈Z}，G={x|x=
+
，p∈Z}，则（ ）
| 1 |
| 6 |
| n |
| 2 |
| 1 |
| 3 |
| p |
| 2 |
| 1 |
| 6 |
| A、E=F?G |
| B、E?F=G |
| C、E⊆F?G |
| D、E?F?G |
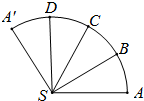如图是圆锥SO（O为底面中心）的侧面展开图，B，C，D是其侧面展开图中弧 |
| AA′ |
| A、∠SAB是直线SA与CD所成的角 |
| B、∠SAC是直线SA与平面ABCD所成的角 |
| C、平面SAC⊥平面SBD |
| D、∠SAD是二面角S-AB-D的平面角 |