题目内容
已知数列{an}中，a1=1，2an+1=an+1，求数列{an}的通项公式an．
考点：数列的概念及简单表示法,数列递推式
专题：点列、递归数列与数学归纳法
分析：把已知的递推式变形，得到an+1-1=
(an-1)，结合a1=1，可得数列{an-1}为常数列0，0，…，则数列{an}的通项公式an可求．
| 1 |
| 2 |
解答：
解：由2an+1=an+1，得2an+1-2=an-1，
∴2（an+1-1）=an-1，即an+1-1=
(an-1)．
∵a1=1，∴a1-1=0，
则a2-1=0，a2=1，
a3-1=0，a3=1，
…
an-1=0，an=1．
∴数列{an}为常数列，an=1．
∴2（an+1-1）=an-1，即an+1-1=
| 1 |
| 2 |
∵a1=1，∴a1-1=0，
则a2-1=0，a2=1，
a3-1=0，a3=1，
…
an-1=0，an=1．
∴数列{an}为常数列，an=1．
点评：本题考查了数列递推式，关键是对递推公式的变形，是中档题．
练习册系列答案
相关题目
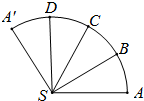如图是圆锥SO（O为底面中心）的侧面展开图，B，C，D是其侧面展开图中弧 |
| AA′ |
| A、∠SAB是直线SA与CD所成的角 |
| B、∠SAC是直线SA与平面ABCD所成的角 |
| C、平面SAC⊥平面SBD |
| D、∠SAD是二面角S-AB-D的平面角 |