题目内容
已知函数f(x)=xlnx,g(x)=k(x-1).
(Ⅰ)若f(x)≥g(x)恒成立,求实数k的值;
(Ⅱ)若方程f(x)=g(x)有一根为x1(x1>1),方程f′(x)=g′(x)的根为x0,是否存在实数k,使
=k?若存在,求出所有满足条件的k值;若不存在,说明理由.
(Ⅰ)若f(x)≥g(x)恒成立,求实数k的值;
(Ⅱ)若方程f(x)=g(x)有一根为x1(x1>1),方程f′(x)=g′(x)的根为x0,是否存在实数k,使
| x1 |
| x0 |
考点:导数在最大值、最小值问题中的应用
专题:综合题,导数的综合应用
分析:(Ⅰ)f(x)≥g(x)恒成立,等价于
≥
恒成立,设h(x)=lnx-
(x>0),求导数,确定函数的最小值h(x)min=h(k)=lnk-k+1≥0,再构造u(x)=lnx-x+1(x>0),求导数,确定函数的单调性,即可得出结论;
(Ⅱ)分类讨论,由(Ⅰ)知当k≤0或k=1时,f(x)=g(x),即h(x)=0仅有唯一解x=1,不合题意;当0<k<1时,h(x)是(k,+∞)上的增函数,对x>1,有h(x)>h(1)=0,所以f(x)=g(x)没有大于1的根,不合题意;当k>1时,由f′(x)=g′(x)解得x0=ek-1,若存在x1=kx0=kek-1,则lnk-1+e1-k=0,证明lnk-1+e1-k=0在(1,+∞)无解,即可得出结论.
| f(x) |
| x |
| g(x) |
| x |
| k(x-1) |
| x |
(Ⅱ)分类讨论,由(Ⅰ)知当k≤0或k=1时,f(x)=g(x),即h(x)=0仅有唯一解x=1,不合题意;当0<k<1时,h(x)是(k,+∞)上的增函数,对x>1,有h(x)>h(1)=0,所以f(x)=g(x)没有大于1的根,不合题意;当k>1时,由f′(x)=g′(x)解得x0=ek-1,若存在x1=kx0=kek-1,则lnk-1+e1-k=0,证明lnk-1+e1-k=0在(1,+∞)无解,即可得出结论.
解答:
解:(Ⅰ)注意到函数f(x)的定义域为(0,+∞),
所以f(x)≥g(x)恒成立,等价于
≥
恒成立,
设h(x)=lnx-
(x>0),
则h′(x)=
,------------(2分)
当k≤0时,h′(x)>0对x>0恒成立,所以h(x)是(0,+∞)上的增函数,
注意到h(1)=0,所以0<x<1时,h(x)<0不合题意.-------(4分)
当k>0时,若0<x<k,h′(x)<0;若x>k,h′(x)>0.
所以h(x)是(0,k)上的减函数,是(k,+∞)上的增函数,
故只需h(x)min=h(k)=lnk-k+1≥0.--------(6分)
令u(x)=lnx-x+1(x>0),u′(x)=
,
当0<x<1时,u′(x)>0; 当x>1时,u′(x)<0.
所以u(x)是(0,1)上的增函数,是(1,+∞)上的减函数.
故u(x)≤u(1)=0当且仅当x=1时等号成立.
所以当且仅当k=1时,h(x)≥0成立,即k=1为所求.--------(8分)
(Ⅱ)由(Ⅰ)知当k≤0或k=1时,f(x)=g(x),即h(x)=0仅有唯一解x=1,不合题意;
当0<k<1时,h(x)是(k,+∞)上的增函数,对x>1,有h(x)>h(1)=0,
所以f(x)=g(x)没有大于1的根,不合题意.---------(8分)
当k>1时,由f′(x)=g′(x)解得x0=ek-1,若存在x1=kx0=kek-1,
则lnk-1+e1-k=0,
令v(x)=lnx-1+e1-x,v′(x)=
,
令s(x)=ex-ex,s′(x)=ex-e,当x>1时,总有s′(x)>0,
所以s(x)是(1,+∞)上的增函数,即s(x)=ex-ex>s(1)=0,
故v′(x)>0,v(x)在(1,+∞)上是增函数,
所以v(x)>v(1)=0,即lnk-1+e1-k=0在(1,+∞)无解.
综上可知,不存在满足条件的实数k.----------------------(12分)
所以f(x)≥g(x)恒成立,等价于
| f(x) |
| x |
| g(x) |
| x |
设h(x)=lnx-
| k(x-1) |
| x |
则h′(x)=
| x-k |
| x2 |
当k≤0时,h′(x)>0对x>0恒成立,所以h(x)是(0,+∞)上的增函数,
注意到h(1)=0,所以0<x<1时,h(x)<0不合题意.-------(4分)
当k>0时,若0<x<k,h′(x)<0;若x>k,h′(x)>0.
所以h(x)是(0,k)上的减函数,是(k,+∞)上的增函数,
故只需h(x)min=h(k)=lnk-k+1≥0.--------(6分)
令u(x)=lnx-x+1(x>0),u′(x)=
| 1-x |
| x |
当0<x<1时,u′(x)>0; 当x>1时,u′(x)<0.
所以u(x)是(0,1)上的增函数,是(1,+∞)上的减函数.
故u(x)≤u(1)=0当且仅当x=1时等号成立.
所以当且仅当k=1时,h(x)≥0成立,即k=1为所求.--------(8分)
(Ⅱ)由(Ⅰ)知当k≤0或k=1时,f(x)=g(x),即h(x)=0仅有唯一解x=1,不合题意;
当0<k<1时,h(x)是(k,+∞)上的增函数,对x>1,有h(x)>h(1)=0,
所以f(x)=g(x)没有大于1的根,不合题意.---------(8分)
当k>1时,由f′(x)=g′(x)解得x0=ek-1,若存在x1=kx0=kek-1,
则lnk-1+e1-k=0,
令v(x)=lnx-1+e1-x,v′(x)=
| ex-ex |
| xex |
令s(x)=ex-ex,s′(x)=ex-e,当x>1时,总有s′(x)>0,
所以s(x)是(1,+∞)上的增函数,即s(x)=ex-ex>s(1)=0,
故v′(x)>0,v(x)在(1,+∞)上是增函数,
所以v(x)>v(1)=0,即lnk-1+e1-k=0在(1,+∞)无解.
综上可知,不存在满足条件的实数k.----------------------(12分)
点评:本题考查导数知识的运用,考查函数的构造,考查函数的最值,考查等价转化问题的能力,属于难题.

练习册系列答案
相关题目
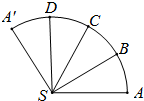 如图是圆锥SO(O为底面中心)的侧面展开图,B,C,D是其侧面展开图中弧
如图是圆锥SO(O为底面中心)的侧面展开图,B,C,D是其侧面展开图中弧 |
| AA′ |
| A、∠SAB是直线SA与CD所成的角 |
| B、∠SAC是直线SA与平面ABCD所成的角 |
| C、平面SAC⊥平面SBD |
| D、∠SAD是二面角S-AB-D的平面角 |