题目内容
已知直线l的倾斜角为120°,并且直线l过点(-3,-2),求直线l的方程.
考点:直线的点斜式方程
专题:直线与圆
分析:由直线的倾斜角求出斜率,用点斜式写出直线方程即可.
解答:
解:∵直线l的倾斜角为120°,
∴直线的斜率为k=tan120°=-
,
又∵直线l过点(-3,-2),
∴直线l的方程为
y+2=-
(x+3),
即
x+y+2+3
=0.
∴直线的斜率为k=tan120°=-
| 3 |
又∵直线l过点(-3,-2),
∴直线l的方程为
y+2=-
| 3 |
即
| 3 |
| 3 |
点评:本题考查了求直线方程的问题,由直线的倾斜角可以得斜率,由斜率与一点可以写出直线方程,是基础题.

练习册系列答案
相关题目
 如图所示,已知椭圆
如图所示,已知椭圆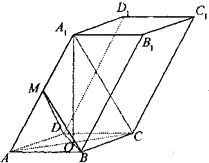 已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,AC∩BD=O,AA1=2
已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,AC∩BD=O,AA1=2